Popis a vizualizace kvantitativních dat
Opět označme pozorované hodnoty sledovaného znaku u n subjektů výběrového souboru jako x1,…, xn. Na rozdíl od kvalitativních dat dochází u kvantitativních dat k opakování pozorování jednotlivých hodnot daného znaku zřídka a tabulku četností, tak jak byla definována výše, nelze pro popis dat použít. Pro použití tabulky četností je třeba nejprve seskupit pozorované hodnoty do m disjunktních, vyčerpávajících a hlavně smysluplných intervalů, které pak v tabulce četností nahrazují kategorie kvalitativního znaku. Znázornění tabulky četností je pak stejné jako v předchozím případě, pro přehlednost je v ní vhodné uvádět i šířku zvolených intervalů (šířku j-tého intervalu budeme značit dj), zejména kvůli srovnatelnosti výsledků.
Příklad 3.2. Uvažujme věk n = 6500 pacientek s karcinomem prsu, který chceme sumarizovat v následujících věkových intervalech: 0–39 let, 40–49 let, 50–59 let, 60–69 let, 70 a více let. Sumarizaci zvolených intervalů, jejich absolutních četností, nj, i relativních četností, nj / n, ukazuje tabulka 3.2.
Tab. 3.2: Věková struktura souboru n = 6500 pacientek s karcinomem prsu
|
Věkový interval
|
dj
|
nj
|
nj / n
|
nj / n (%)
|
|
0-39 let
|
40
|
231
|
0,036
|
3,6 %
|
|
40-49 let
|
10
|
747
|
0,115
|
11,5 %
|
|
50-59 let
|
10
|
1559
|
0,240
|
24,0 %
|
|
60-69 let
|
10
|
1894
|
0,291
|
29,1 %
|
|
70 a více let
|
20
|
2069
|
0,318
|
31,8 %
|
|
Celkem
|
90
|
6500
|
1
|
100 %
|
Míry polohy
I když nám frekvenční tabulka zpřehledňuje pozorované hodnoty a umožňuje zjistit, kterých hodnot je v našem souboru více a kterých naopak méně, je vhodné ji vždy doplnit statistikou, která shrnuje soubor dat jedním číslem a představuje „typickou hodnotu“, kolem které mají ostatní pozorované hodnoty tendenci kolísat. Nejčastěji jsou jako charakteristiky polohy používány statistiky průměr (mean) a medián (median). Průměr neboli aritmetický průměr či výběrový průměr lze jednoduše spočítat jako součet pozorovaných hodnot dělený jejich počtem:
|
|
(3.1) |
Abychom mohli definovat medián, je třeba kromě neuspořádaného výběrového souboru x1,…, xn uvažovat i jeho uspořádanou variantu x(1) ≤ x(2) … ≤ x(n), kde x(1) značí minimální pozorovanou hodnotu a x(n) značí maximální pozorovanou hodnotu. Medián pak definujeme následovně:
|
|
(3.2) |
|
|
Z výše uvedeného je vidět, že zatímco průměr je vypočten ze všech pozorovaných hodnot a všechny hodnoty souboru se tak podílejí na jeho výsledné číselné realizaci, medián je prostřední pozorovaná hodnota, která dělí celý soubor na dvě poloviny, tedy polovina souboru je menší než medián a naopak polovina souboru je větší než medián. S těmito vlastnostmi obou statistik jsou spojeny jejich výhody i nevýhody.
Chceme-li, aby naše vypočtená statistika byla dobrým odhadem frekvenčního středu dat, je medián vždy dobrou volbou. Průměr je v tomto případě dobrou volbou pouze tehdy, když jsou naše data symetrická a neobsahují odlehlé či nesprávné hodnoty. V případě asymetrických dat nebo přítomnosti odlehlých hodnot má totiž průměr tendenci se těmto „netypickým“ hodnotám přizpůsobovat, což ho jako odhad frekvenčního středu dat diskvalifikuje. Typickým příkladem pro vysvětlení této vlastnosti průměru je výpočet průměrného platu v České republice. Je totiž zřejmé, že průměrný plat není dobrým odhadem středního výdělku české populace, neboť jeho hodnota je značně ovlivněna malou skupinou lidí s velmi vysokými příjmy. Medián je na druhou stranu dobrým odhadem středního výdělku české populace, protože jednoznačně určuje frekvenční střed dosahovaných příjmů. Problematickou situací pro obě míry, tedy průměr i medián, jsou data se dvěma (případně více) frekvenčními středy, kde může být zavádějící použití obou měr. V tomto případě by mělo primárně dojít k analýze toho, co způsobuje toto chování, a případně by mělo dojít k adekvátnímu rozdělení souboru (může se nám např. stát, že máme ve výběrovém souboru dvě homogenní skupiny, které se však ve sledovaném znaku vzájemně liší).
Jako míry polohy lze použít i minimální (hodnota x(1)) a maximální (hodnota x(n)) pozorované hodnoty, které nám také dávají obraz o tom, kde se námi sledovaná náhodná veličina X pohybuje na reálné ose. S uspořádanou variantou výběrového souboru, tedy s hodnotami x(1) ≤ x(2) … ≤ x(n) souvisí i další důležitý pojem statistiky a analýzy dat, a to pojem kvantil (percentile). Ve statistice je kvantil definován pomocí kvantilové funkce, laicky lze kvantil definovat jako číslo na reálné ose, které rozděluje pozorované hodnoty na dvě části dle pravděpodobnosti. Jinak řečeno, tzv. p% kvantil (p-procentní kvantil) rozděluje data na p procent hodnot a (100 – p) procent hodnot, kdy p procent hodnot je menších (nebo rovno) než p% kvantil a naopak (100 – p) procent hodnot je větších (nebo rovno) než p% kvantil. Mluvíme-li o p% kvantilu pozorovaných hodnot, je třeba si uvědomit, že se vždy jedná o jednu z naměřených hodnot, tedy jednu z hodnot x(1) ≤ x(2) … ≤ x(n), případně o průměr dvou takových sousedních hodnot. Označíme-li p% kvantil jako xp/100, můžeme ho mezi seřazenými hodnotami najít následovně:
|
|
(3.3) |
|
|
přitom představuje horní celou část čísla np/100.
Příklad nalezení 80% kvantilu hodnot výšky v souboru 20 osob ukazuje obrázek 3.2. Významnými kvantily jsou již zmíněné minimální (0% kvantil) a maximální (100% kvantil) pozorovaná hodnota a medián (50% kvantil), kromě nich jsou ještě používány hodnoty 25% a 75% kvantilu, které se standardně nazývají dolní a horní kvartil (lower and upper quartile).
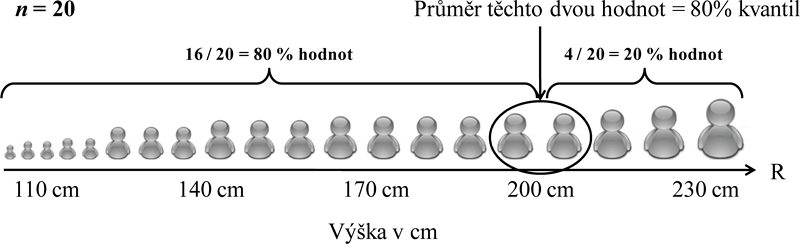
Obr. 3.2: Příklad nalezení 80% kvantilu hodnot výšky v souboru 20 osob.
Míry variability
Výpočet míry polohy jako „typického“ pozorování je nezbytné doplnit také informací o tom, jak jsou kolem této hodnoty rozložena ostatní pozorování, což znamená doplnit míru polohy tzv. mírou variability. Důvod je zřejmý, je třeba od sebe odlišit dva znaky, které nabývají stejné průměrné hodnoty (např. 50), ale zásadně se liší ve spektru hodnot, jež tento znak může nabývat. Ve chvíli, kdy první znak může nabývat např. hodnot od 0 do 100 a druhý od 40 do 60, je jasné, že první znak vykazuje větší variabilitu než znak druhý, což bychom nebyli z pouhé znalosti průměru schopni zjistit. Jak již bylo naznačeno, nejjednodušší charakteristikou variability pozorovaných dat je rozsah hodnot (range), který je dán minimální a maximální pozorovanou hodnotou. Nevýhodou prezentování rozsahu pozorovaných hodnot je jeho náchylnost k netypickým, odlehlým, případně chybným hodnotám. Tento fakt lze na druhou stranu využít právě pro identifikaci problematických hodnot a čištění datového souboru ještě před začátkem jakéhokoliv statistického zpracování.
Další mírou variability, která není téměř vůbec náchylná na odlehlá pozorování je tzv. kvantilové rozpětí, což je interval definovaný hodnotami p% kvantilu a (100 – p)% kvantilu. Speciálním případem kvantilového rozpětí je tzv. kvartilové rozpětí (interquartile range, IQR), které je dáno dolním a horním kvartilem a které pokrývá 50 % pozorovaných hodnot.
Rozsah hodnot i kvantilové rozpětí nám sice dávají informaci o variabilitě, ale v obou případech se jedná o charakteristiky vypočtené na základě dvou pozorování, které nezohledňují polohu „typického“ pozorování, např. průměru nebo mediánu. Fluktuaci pozorovaných hodnot kolem průměru odráží výběrový rozptyl (sample variance), značíme ho s2, a je definován jako průměrný kvadrát odchylky pozorovaných hodnot od hodnoty průměru:
|
|
(3.4) |
Je třeba poznamenat, že ve jmenovateli vzorce (3.4) pro výběrový rozptyl je výraz n – 1 a nikoliv n. Jedná se o výpočetní korekci, která má zamezit podhodnocení výběrového rozptylu u malých výběrových souborů a která je známa pod označením Besselova korekce. Výběrový rozptyl trpí stejnou nevýhodou jako průměr, a to citlivostí na odlehlé a chybné hodnoty, která je ještě zvýrazněna druhou mocninou. Výběrový rozptyl má navíc interpretační nevýhodu v tom, že nemá stejné jednotky jako pozorované hodnoty a jejich průměr, a proto se častěji jako míra variability používá jeho odmocnina, tzv. výběrová směrodatná odchylka (sample standard deviation), kterou značíme s.
Příklad 3.3. Naším cílem je vypočítat průměr, medián a výběrovou směrodatnou odchylku hladiny cholesterolu vybrané populace mužů (n = 22). Naměřené hodnoty jsou uvedeny v mmol/l a jsou dány v tabulce 3.3.
Tab. 3.3: Hodnoty cholesterolu vybrané populace mužů (mmol/l).
| 6.2 | 7.6 | 6.3 | 9.1 | 4.2 | 5.8 | 5.65 | 6.3 | 8.6 | 6.0 | 6.2 |
| 6.7 | 4.6 | 6.25 | 6.4 | 4.04 | 6.3 | 9.1 | 6.3 | 5.2 | 6.4 | 5.75 |
Výpočet požadovaných statistik (v mmol/l) je pak následující:
Průměr: Medián: (3.5) Směrodatná odchylka:
Bodový graf
Bodový graf (scatter plot) je grafický nástroj pro vizualizaci kvantitativních dat zobrazující každou měřenou hodnotu jako bod plochy. Lze ho použít na vizualizaci naměřených hodnot v několika kategoriích (od jedné až po mnoho), ale jeho největší přínos je zejména ve vizualizaci vzájemného vztahu dvou veličin spojitého typu, kdy hodnoty jedné veličiny jsou zobrazeny na ose x a hodnoty druhé veličiny jsou zobrazeny na ose y.
Histogram
Neocenitelným a možná nejpoužívanějším grafickým nástrojem pro vizualizaci poměrových a intervalových dat je tzv. histogram (histogram). Histogram vzhledem připomíná sloupcový graf, ale na rozdíl od sloupcového grafu každý sloupec v histogramu odráží absolutní nebo relativní četnost na jednotku sledované veličiny na vodorovné ose. Naproti tomu sloupcový graf znázorňuje kvalitativní data a jako takový s žádnými jednotkami na vodorovné ose nepracuje; na kvantitativní data jej lze použít až po jejich kategorizaci (agregaci do intervalů).
Máme-li n hodnot sledované veličiny u výběrového souboru: x1,…, xn, je třeba je pro vytvoření histogramu nejdříve seřadit dle velikosti a rozdělit do m vzájemně disjunktních intervalů, které vytvoříme na vodorovné ose. Šířku j-tého intervalu označíme jako dj a počet pozorovaných hodnot, které padly do j-tého intervalu, označíme symbolem nj. Výšku sloupců histogramu pro j-tý interval pak můžeme vyjádřit pomocí relativní četnosti jako
|
|
(3.6) |
nebo pomocí absolutní četnosti jako
|
|
(3.7) |
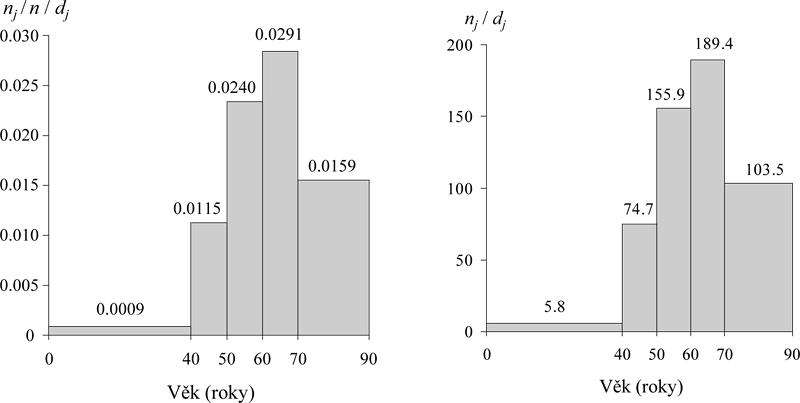
Příklad 3.4. Vraťme se k datům o věku 6500 pacientek s karcinomem prsu z příkladu 3.2 a sestrojme histogram s použitím věkových kategorií: 0–39 let, 40–49 let, 50–59 let, 60–69 let, 70 a více let. Pozorované absolutní a relativní četnosti i hodnoty f(j) a f *(j) nezbytné pro sestrojení histogramu sumarizuje tabulka 3.4, histogramy pro absolutní a relativní četnost s použitím dat z tabulky 3.4 ukazuje obrázek 3.3.
Tab. 3.4: Věková struktura souboru n = 6500 pacientek s karcinomem prsu
| Věkový interval | dj | nj | nj / n | nj / dj | nj / n / dj |
| 0-39 let | 40 | 231 | 0,036 | 5,8 | 0,0009 |
| 40-49 let | 10 | 747 | 0,115 | 74,7 | 0,0115 |
| 50-59 let | 10 | 1559 | 0,240 | 155,9 | 0,0240 |
| 60-69 let | 10 | 1894 | 0,291 | 189,4 | 0,0291 |
| 70 a více let | 20 | 2069 | 0,318 | 103,5 | 0,0159 |
| Celkem | 90 | 6500 | 1 | - | - |
Přepočet absolutních a relativních četností na šířku intervalu vypadá na první pohled zbytečně, nicméně důvody pro tento výpočet jsou dva:
- Přepočet na šířku intervalu zajišťuje zároveň jejich srovnatelnost vzhledem k absolutním i relativním četnostem. Příkladem může být srovnání četností věkových kategorií 60–69 let a 70 a více let v tabulce 3.4. Z hlediska absolutní i relativní četnosti nestandardizované na šířku intervalu se zdá být věkový interval 70 a více let četnější než interval 60–69 let, je to ale dáno tím, že zahrnuje širší věkové spektrum. Po standardizaci na šířku intervalu je vidět, že četnější je naopak věková kategorie 60–69 let.
- Celková plocha histogramu pro absolutní četnost je rovna celkové velikosti výběru, zatímco celková plocha histogramu pro relativní četnost je rovna 1. Tato skutečnost má těsnou vazbu na základní popis pravděpodobnostního chování náhodné veličiny, kterým je hustota rozdělení pravděpodobnosti (density function). Ta je definována spolu s dalšími charakteristikami náhodné veličiny v následující kapitole, nicméně je třeba poznamenat, že histogram lze chápat jako odhad tvaru hustoty pravděpodobnosti. Jinými slovy, je to grafická vizualizace pravděpodobnostního chování kvantitativních (zejména spojitých) dat.
Obr. 3.3: Histogram pro relativní četnost (vlevo) a absolutní četnost (vpravo) z příkladu 3.4.
Na druhou stranu, v dnešním statistickém software je histogram zřídka vyjadřován pomocí výrazů 3.6 a 3.7. Daleko častěji se jedná o prosté absolutní nebo relativní počty pozorování v daném intervalu, které jsou výhodné zejména kvůli snadné čitelnosti a interpretaci. Abychom však byli schopni adekvátní interpretace, je důležité, aby intervaly měly stejnou šířku, a to z důvodu srovnatelnosti, který byl popsán výše.
Dalším důležitým aspektem tvorby histogramu je počet jeho intervalů, neboť ten v zásadě rozhoduje o tom, jak bude histogram vypadat. Při malém počtu intervalů může být charakter dat maskován, zatímco při velkém počtu intervalů zase můžeme pozorovat velkou variabilitu v četnostech jednotlivých intervalů. Jak tedy volit počet intervalů? Nejčastěji jsou používány dvě jednoduché metody, kdy v prvním případě volíme počet intervalů (m) roven odmocnině z celkového počtu pozorování, tedy m = √n, v druhém případě pak podle tzv. Sturgesova pravidla volíme počet intervalů jako 1 + logaritmus o základu dva z celkového počtu pozorování, tedy m = 1 + log2(n).
Krabicový graf
Dalším nástrojem pro vizualizaci kvantitativních dat je tzv. krabicový graf (box plot), což je, jak název napovídá, graf ve tvaru obdélníku doplněný tzv. fousky. Jednotlivé prvky krabicového grafu nejčastěji odpovídají významným kvantilům vypočteným na základě pozorovaných dat (obrázek 3.4). Uvnitř obdélníkového tvaru je naznačena pozice mediánu (50% kvantilu) a obdélník samotný značí polohu dolního a horního kvartilu, tedy 25% a 75% kvantilu. Tyto dva kvantily odpovídají kvartilovému rozpětí, které ohraničuje 50% pozorovaných hodnot. Fousky dosahující za hranice obdélníkového tvaru pak signalizují polohu hodnot více vzdálených od mediánu, nejčastěji odpovídají 5% kvantilu (spodní fousek) a 95% kvantilu (horní fousek), případně minimu a maximu pozorovaných hodnot.
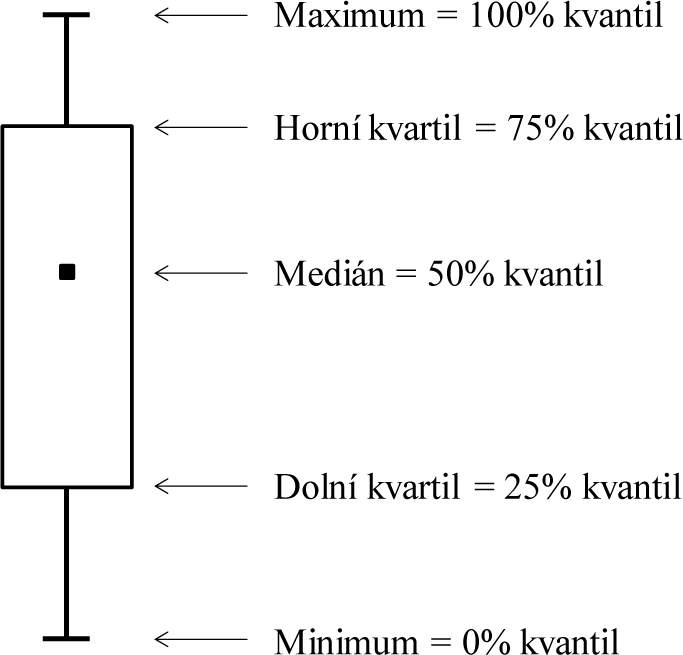
Obr. 3.4: Příklad krabicového grafu s vyznačením významných kvantilů pozorovaných dat.