Logaritmicko-normální rozdělení

S logaritmicko-normálním (log-normálním) rozdělením (log-normal distribution) se na rozdíl od dvou předchozích rozdělení můžeme relativně často setkat v přírodě (respektive jak v biologii, tak v medicíně). Logaritmicko-normální rozdělení má např. tělesná hmotnost, délka inkubační doby infekčního onemocnění nebo abundance živočišných druhů. V neposlední řadě toto rozdělení charakterizuje i řadu krevních parametrů (např. počet krevních buněk v daném objemu, sérový bilirubin u pacientů s cirhózou). Náhodná veličina X má logaritmicko-normální rozdělení právě tehdy, když veličina Y = ln(X) má normální rozdělení (výraz ln zde zastupuje přirozený logaritmus). A to samé platí i naopak, když veličina Y má normální rozdělení, pak náhodná veličina X = exp(Y) má rozdělení logaritmicko-normální. Hustota je dána vztahem

(4.19)

kde parametry µ a σ² mají význam střední hodnoty a rozptylu normálního rozdělení odpovídající náhodné veličiny Y = ln(X). Ukázky hustot logaritmicko-normálního rozdělení pro čtyři různé kombinace parametrů µ a σ² jsou zobrazeny na obrázku 4.5 vlevo. Logaritmicko-normální náhodná veličina X opět nabývá pouze nezáporných hodnot, platí tedy f(x) = 0 pro x < 0.

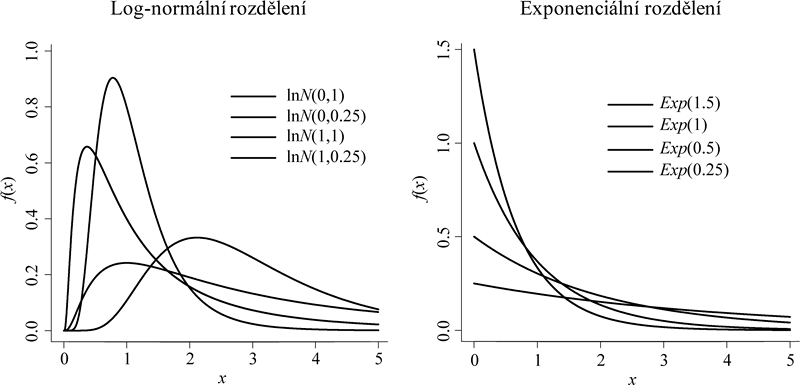
Obr. 4.5: Ukázky hustot náhodných veličin s log-normálním a exponenciálním rozdělením.