
Studentovo t rozdělení
Studentovo t rozdělení (Student’s t-distribution) je také spojité rozdělení pravděpodobnosti, které stejně jako v předchozím případě nachází spíše uplatnění v teoretické statistice než v přírodě [2]. Toto rozdělení charakterizuje rozdělení pravděpodobnosti průměru jako odhadu střední hodnoty veličiny s normálním rozdělením v případě, že neznáme přesnou hodnotu rozptylu (což je v praktickém životě téměř vždy). Studentovo t rozdělení vzniká jako podíl dvou nezávislých náhodných veličin, jedné s rozdělením N(0,1) a druhé s rozdělením χ2(k). Platí tedy:
|
|
(4.18) |
Parametrem Studentova t rozdělení je opět počet stupňů volnosti k, který přebírá od rozdělení chí-kvadrát. Studentovo rozdělení lze také chápat jako aproximaci standardizovaného normálního rozdělení pro malé výběrové soubory (tomu odpovídá malá hodnota parametru k), s rostoucí velikostí souboru (s rostoucím parametrem k) se hustota Studentova rozdělení (a tedy i kvantily) přibližuje hustotě normálního rozdělení. Srovnáním obrázku 4.4 vpravo s obrázkem 4.3 lze zjistit, že již pro k = 100 je hustota Studentova t rozdělení téměř shodná s hustotou standardizovaného normálního rozdělení.
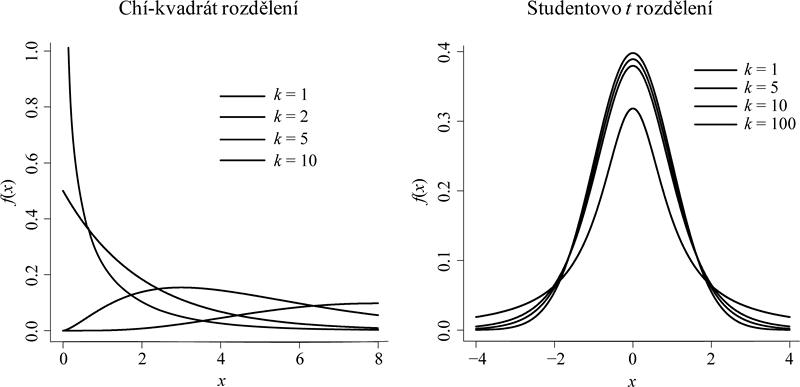
Obr. 4.4: Ukázky hustot náhodných veličin s chí-kvadrát rozdělením a Studentovým t rozdělením.




