
Popis a vizualizace kvalitativních dat
Označme x1,…, xn zaznamenané hodnoty sledovaného znaku u výběrového souboru n subjektů. U kvalitativních dat předpokládáme opakování pozorování jednotlivých hodnot daného znaku, proto je logické sumarizovat tato data pomocí tabulky s četnostmi možných hodnot (tabulka četností, frequency table). Označíme-li y1,…, ym možné hodnoty sledovaného znaku, pozorovanou (absolutní) četnost odpovídající variantě znaku yj budeme označovat jako nj. Pro lepší orientaci a možnost srovnání je vhodné doplnit pozorovanou četnost i relativní četností, která má pro variantu znaku yj tvar nj / n.
Příklad 3.1. Sledujeme přítomnost diabetu u pacientů zdravotnického zařízení za období jednoho roku s tím, že rozlišujeme pacienta bez diabetu a pacienty s diabetem 1. nebo 2. typu (m = 3). Celkem bylo pozorováno n = 687 pacientů, sumarizaci výsledků uvádí tabulka 3.1.
Tab. 3.1: Počty pacientů ve zdravotnickém zařízení dle přítomnosti diabetu
Přítomnost diabetu yj nj nj / n nj / n (%) Bez diabetu 0 621 0,904 90,4 % Diabetes 1. typu 1 8 0,084 1,2 % Diabetes 2. typu 2 58 0,012 8,4 % Celkem 687 1 100 %
Vzhledem k tomu, že kvalitativní data často nelze seřadit dle velikosti, používá se jako frekvenční charakteristika těchto dat tzv. mód (mode), což je varianta znaku s největší četností. V příkladu 3.1 je modální hodnotou pacient bez diabetu. Vypovídací hodnota módu jako reprezentanta pozorovaných dat závisí především na počtu kategorií sledovaného znaku a vyrovnanosti jejich četností. Někdy může být mód opravdu typickou hodnotou, jindy mohou být četnosti jednotlivých variant znaku tak vyrovnané, že to spíše indikuje neexistenci typické hodnoty pro daný znak.
V případě nízkých pozorovaných četností některých kategorií je často vhodné tyto kategorie sloučit a dále pracovat již pouze se sloučenými kategoriemi. Slučovat by se však měly pouze sousední kategorie a ještě pouze v případě, kdy jejich sloučení zachovává data interpretovatelnými.
Pro vizualizaci kvalitativních dat se nejčastěji používají sloupcový graf (bar plot) a výsečový neboli koláčový graf (pie chart), kde výška sloupců (šířka je pro všechny sloupce stejná), respektive plocha výsečí, pro jednotlivé varianty je úměrná jejich četnosti. U koláčového grafu jeho plocha představuje 100 %, proto je vhodný pro vizualizaci relativních četností, ve sloupcovém grafu můžeme zobrazit obojí, jak absolutní, tak relativní četnosti. Příklad sloupcového a koláčového grafu s absolutními a relativními četnostmi z tabulky 3.1 je uveden na obrázku 3.1.
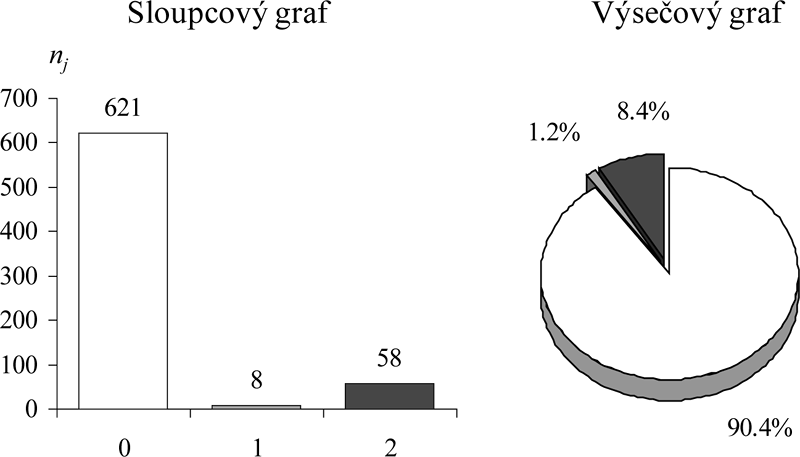
Obr. 3.1: Příklad sloupcového a výsečového grafu na datech z tabulky 3.1.




