Využití markovských řetězců v analýze biodiverzity

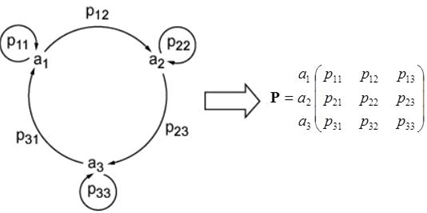
Složitějším přístupem, který do hodnocení společenstev zavádí i pojem času, jsou markovské řetězce. Markovské řetězce popisují systémy, které jsou definovány svými stavy, které nastávají v různém čase , přičemž mezi stavy (např. typ společenstva na lokalitě) existuje pravděpodobnost přechodu (Obr. 9.3). Může být popsán pomocí přechodové matice:

kde , je pravděpodobnost přechodu ze stavu do stavu v jednom časovém kroku systému. Pro přechodovou matici platí, že součet v jejích řádcích je vždy jedna.  Na základě znalosti stavu systému na počátku a přechodové matice P můžeme zjistit stav systému v čase n kroků pomocí jednoduchého vzorce . V případě dodržení určitých podmínek pro matici P (regulární matice) je pro matici možné spočítat takzvaný pevný bod w, pro který platí , interpretace tohoto pevného bodu je, že jde o stabilní poměr stavů , ke kterému systém (za předpokladu, že matice P je regulární, což lze snadno ověřit) směřuje za dlouhý počet kroků. Pevný bod tedy představuje poměr stavů systému (např. ve významu typů společenstev), který se v dlouhodobém horizontu stabilizuje.

Výše popsaný markovský řetězec představuje nejjednodušší případ, kdy se přechodová matice P nemění s časem, jde o takzvaný homogenní markovský řetězec. Markovský řetězec může obsahovat také takzvané absorbující stavy, to jsou stavy, z nichž se už systém nemůže dostat jinam (úmrtí jedince, zánik lokality apod.). Kromě homogenních existují ještě nehomogenní markovské řetězce, které používají při výpočtu několik přechodových matic, typickým příkladem jsou cyklické jevy, jako je střídání ročních období. Při různých přechodech, kde , pak pro přechodovou matici P platí , kde je číslo přechodu. Kromě výhod definice stabilního stavu systému a predikce jeho stavu mají markovské řetězce také nevýhody. Pro analýzu společenstev je nejkritičtější potřeba velkých souborů dat, které by navíc měly být získávány po dlouhé časové období. Markovské řetězce jsou používány pro modelování řady biologických jevů, mimo jiné i pro modelování stavu společenstev. Nehomogenní markovské řetězce byly použity s dobrými výsledky například pro studium změn společenstev zoobentosu v jednotlivých ročních obdobích. V parazitologii jsou markovské řetězce využívány často pro modelování dynamiky infekcí a v epidemiologii.