Zipfovy-Mandelbrotovy modely
Nespokojenost s existujícími modely heterogenity společenstva přiměla řadu ekologů k hledání dalším možných modelů pro lepší popis těchto vztahů.
Jedním z takto získaných modelů je i Zipfův-Mandelbrotův model, který má podobně jako Shannonův-Weaverův index základ v lingvistické a informační teorii. Zipfův zákon popisuje pořadí slov podle frekvence jejich výskytu v textu. G. K. Zipf studoval otázky statistického rozložení slov v textu. Zjistil, že když vynese logaritmy frekvence nejčastěji se vyskytujících slov proti logaritmu jejich pořadí, tvoří body na počátku grafu zcela přijatelnou přímku. Konec představovaný řídce se vyskytujícími slovy potom začne od přímky odpadat. Zipf použil pořadovou statistiku:
|
|
(1) |
kde a
jsou konstanty a
je nezávislá proměnná. Kvůli lepšímu dosazení dat navrhl Mandelbrot jeho zobecnění
|
|
(2) |
kde ,
a
jsou konstanty. Zipfovo-Mandelbrotovo rozložení, které vzniklo v kontextu statistické mechaniky, může být obecně zapsáno takto:
|
|
(3) |
kde ,
a
jsou reálné parametry. Tato funkce při lim
přechází v normální exponenciální rozložení
|
|
(4) |
Navíc tato funkce vyhovuje rovnici normálního rozložení:
|
|
(5) |
|
|
|
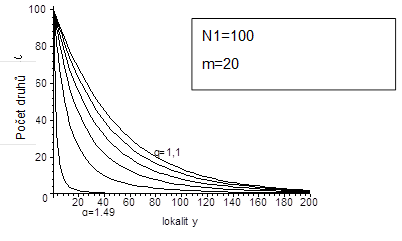
Obr. 6.3: Simulace vlivu q na tvar Zipfova-Mandelbrotova rozložení |
Příkladem využití může být modelování počtu vzácných druhů na lokalitách. Nejprve, aby mohly být odstraněny a
, je třeba vyjádřit počet lokalit se vzácnými taxony, s výskytem pouze jednoho jedince a průměrný počet taxonů na lokalitu. Mimoto je také dobré nahradit diskrétní průměr spojitým:
|
|
(6) |
Parametr může být považován za míru normality rozložení, s rostoucím
se zvětšuje zakřivení paraboly (obr. 6.3). Po předchozích úpravách může být rovnice 3 pro rozložení taxonů přepsána jako:
|
|
(7) |
V ekologickém podání je obecně známa interpretace Zipfových-Mandelbrotových modelů odrážející sukcesní proces, ve kterém pozdní kolonizátoři mají více specifické požadavky a jsou proto vzácnější než druhy, jenž obsadily prostor dříve. Model předpokládá pevně dané pořadí kolonizátorů se stejnými druhy přítomnými ve stejném bodě sukcese v podobných habitatech, ovšem v reálných podmínkách tento předpoklad není vždy dodržen. Přestože model není přesný ve společenstvech s velkým množstvím vzácných druhů, byl model úspěšně aplikován na řadu společenstev.