Stavová mapa přechodů

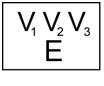
Proces aktivní dynamiky pro konkrétní Hopfieldovu síť můžeme zobrazit pomocí stavové mapy přechodů. Každý uzel v této mapě obsahuje informaci o aktuálním stavu sítě a také energii, která tomuto stavu odpovídá.

Obr. 4. Uzel ve stavové mapě přechodů a jeho obsah

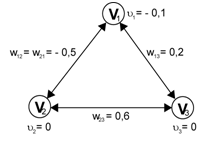
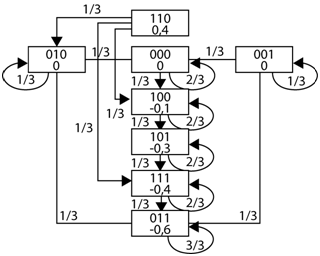
Jednotlivé uzly je možné v diagramu uspořádat od uzlů s nejvyšší energií až po uzly s energií nejnižší. Přiložení vstupu na síť odpovídá nastavení sítě do stavu rovnajícímu se tomuto vstupu. Pokud budeme předpokládat síť, kde jsou jednotlivé neurony voleny diskrétně a náhodně se stejnou pravděpodobností,můžeme Hopfieldovu síť a její mapu přechodů zobrazit následovně:

Obr. 5. Hopfieldova síť se třemi uzly a odpovídající mapa přechodů

Hrany mezi jednotlivými uzly odpovídají pravděpodobnosti, s jakou je ten který přechod proveden. V našem případě je výběr každého ze tří neuronů stejně pravděpodobný. Po jistém počtu kroků se síť dostane do stavu vyjádřeného jako 011, který odpovídá minimální hodnotě energie sítě a je v tomto případě dokonce globálním atraktorem. Ať je již v tomto stavu zvolen/aktivován kterýkoli z neuronů, nezmění svůj stav a síť tedy zůstává v tomto stabilním stavu.