Vícevrstvý perceptron a syndrom přeučení

Vícevrstvý perceptron je univerzálním robustním výpočetním modelem, který představuje vzhledem k platnosti Kolmogorova teorémupro vícevrstvý perceptron velmi univerzální řešení. Praktické je zejména jeho použití v případech, kdy máme k dispozici jen příklady vstupů a výstupů nějakého procesu.  Velká vyjadřovací síla vícevrstvého perceptronu je však vykoupena poměrně výpočetně náročnou optimalizací sítě pomocí BP algoritmu. Mezi nevýhody také patří, že nalezená transformace je ve struktuře sítě ukryta, nelze ji přímo jednoduše interpretovat jako sadu analytických pravidel, nalezená transformace je dle Kolmogorova teorému v síti vyjádřena lineární kombinací jednoduchých spojitých nelineárních funkcí jedné proměnné.

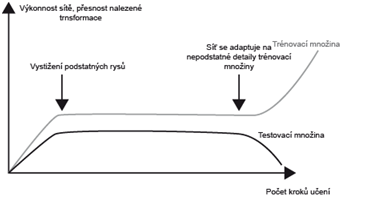
Nalezení globálního minima chybové funkce přes trénovací množinu není také vždy účelné. Může dojít k tzv. efektu přeučení sítě, kdy síť sice efektivně minimalizuje chybovou funkci přes trénovací množinu, nicméně na úkor obecnosti nalezené transformace pro vzory mimo trénovací množinu. Síť se adaptovala na nepodstatné detaily obsažené v trénovací množině. Taková přeučená síť pak není schopna zobecňovat, jak je vidět na poklesu výkonnosti sítě vzhledem k testovací množině.

Obr. 17. Syndrom přeučení

Přeučení sítě lze bránit několika postupy. Je výhodné nesnažit se dosáhnout absolutního minima chybové funkce přes celou trénovací množinu, ale učení sítě zastavit o jistý okamžik dříve. Tento okamžik lze velmi často odhadnout jako náhlý pokles hodnoty chybové funkce nad trénovací množinou. Ještě efektivnějším postupem bránícím přeučení bývá zavedení nejen trénovací a testovací množiny, ale i množiny validační, která adaptaci včas zastaví. 

Dále se při návrhu perceptronu snažíme volit pokud možno malý počet neuronů ve skrytých vrstvách, to povede síť ke hledání jednodušší a obecnější transformace. Aby se síť nesoustředila na vystižení nepodstatných detailů trénovací množiny, je možné předkládané vstupy vždy nepatrně zkreslit, například náhodným šumem.