
Organizační dynamika
Organizační dynamika Boltzmannova stroje je naprosto stejná jako u Hopfieldovy sítě, nejčastěji Hopfieldovy sítě se skrytými neurony. Rozdíl je v typu použitých neuronů. Ty se nechovají deterministicky, jako v případě Hopfieldovy sítě, ale změna stavu neuronu na opačný ( a
) závisí nejen na hodnotě aktivační funkce, ale také na veličině nazývané teplota sítě
Tato teplota se obvykle mění v průběhu práce sítě a je zodpovědná za stochastické chování neuronů a energie sítě tak nemusí na rozdíl od Hopfieldovy sítě v každém kroku sítě jen klesat.
Základem Boltzmannova stroje je tedy stochastický neuron, u kterého známe pravděpodobnost se kterou se bude nacházet v daném stavu na základě hodnoty vnitřního potenciálu neuronu. Funkcí vyjadřující závislost pravděpodobnosti změny stavu je často sigmoida, která je modifikována právě parametrem
V závislosti na teplotě tedy může stochastický neuron s jistou pravděpodobností změnit svůj stav bez ohledu na hodnotu vnitřního potenciálu
|
|
(14) |
Pro dostáváme pro pravděpodobnost změny stavu standardní sigmoidální funkci a neuron se tedy s vysokou pravděpodobností bude chovat dle hodnoty svého vnitřního potenciálu
Ze vztahu Sítě se vzájemnými vazbami (14) dále vyplývá, že s rostoucí hodnotou parametru
dochází k vyrovnání pravděpodobnosti volby obou stavů bez ohledu na hodnotu vnitřního potenciálu
a pro
se neuron chová zcela náhodně, oba stavy jsou stejně pravděpodobné.
 |
|
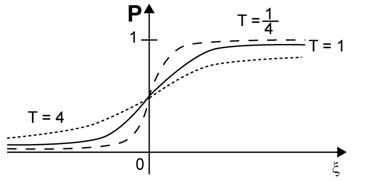
Obr. 7. Průběh pravděpodobnostní aktivační funkce v závislosti na T a
|




