Hodnocení metod

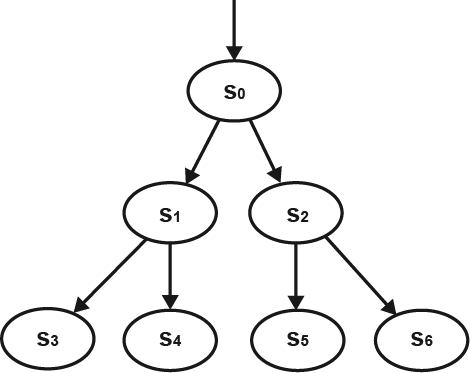
Pokud chceme zvolit vhodnou metodu prohledávání stavového prostoru, musíme mít možnost tyto metody popsat a porovnávat. K tomu nám slouží základní parametry metod, které je charakterizují. Předpokládejme orientovaný graf, který metoda prohledává ve formě stromu zobrazeného na následujícím obrázku.

Obr. 4. Prohledávací strom. Uzel je představován příslušným stavem úlohy a dalšími informacemi nutnými pro prohledávání daným algoritmem.

Zaveďme si následující pojmy:

1. Faktor větvení, značíme
2. Hloubka cíle, značíme
3. Maximální délka cesty, značíme

Ad a) Faktor větvení udává, kolik následníků může být průměrně z každého stavu vygenerováno. V případě hodnocení výkonnosti nějaké heuristiky, používáme i pojem efektivní faktor větvení, označovaný jako Efektivní faktor větvení udává takovou hodnotu větvení, která by po nalezení cíle v hloubce a počtu expandovaných stavů odpovídala rovnoměrně vyváženému stromu hloubky s počtem stavů (uzlů) V případě zcela ideální heuristiky by byl efektivní faktor větvení roven jedné.

Ad b) Hloubka cíle označuje počet úrovní stromu, kterými musíme stromem od kořene (počáteční stav) k cíli na nejnižší úrovni projít.

Ad c) Hloubka je počítána od kořene, který leží v úrovni 0. Maximální délka cesty odpovídá nejdelší možné cestě ve stavovém prostoru, která je při prohledávání realizována (generována).

U metod prohledávání stavového prostoru se budeme zajímat, zda

1. je metoda úplná,
2. je optimální,
3. jaká je její časová složitost,
4. jaká je její prostorová složitost.

Ad a) Říkáme, že metoda je úplná, pokud nalezne řešení vždy, když existuje.

Ad b) Optimální metoda nalezne navíc řešení nejlepší.  Nalezne tedy řešení s nejkratší cestou v případě uniformě ohodnocených hran přechodů, respektive řešení s nejnižší cenou těchto přechodů v případě jejich neuniformního ohodnocení.

Ad c) Časová složitost udává, v kolika krocích, tedy kolika aplikacích operátorů přechodu bude řešení nalezeno.

Ad d) Podobně prostorová složitost říká, kolik paměti, obvykle ve smyslu počtu uchovávaných stavů, bude pro algoritmus zapotřebí.

To nám umožní každý algoritmus pro prohledávání stavového prostoru charakterizovat z pohledu záruky nalezení (nejlepšího) řešení. Parametry časové a prostorové složitosti umožní odhadnout reálnou náročnost jejich implementace na PC z pohledu potřebného strojového času procesoru (časová složitost) a z pohledu potřebné operační paměti počítače (prostorová složitost).