
Realizace logické funkce XOR
Předcházející odstavec demonstroval, že výpočetní síla jednotlivého neuronu je zcela dostatečná pro výpočet logických funkcí AND, OR a NOT. Jaká je situace v případě realizace logické funkce XOR (exlusivní OR)?
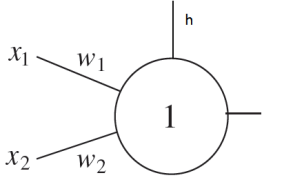
Předpokládejme stejný neuron jako v předcházejícím případě, pouzepro zjednodušenís prahem označeným jako (víme, že je realizován vahou
a konstantní vstupem
).
 |
|
Obr. 12. Neuron pro realizaci funkce OR a NOT.
|
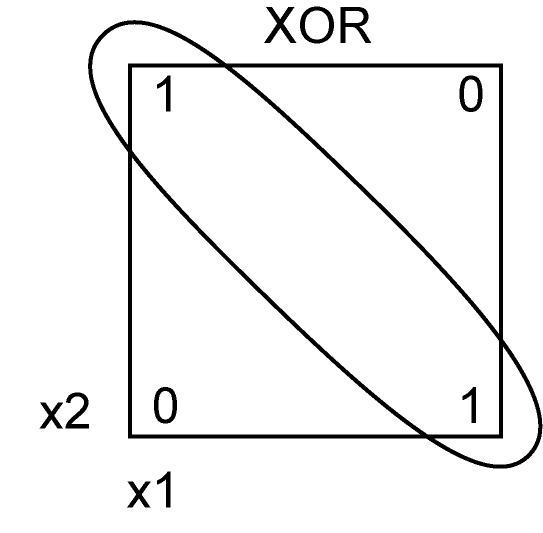
Tabulka hodnot funkce XOR a její grafické znázornění je uvedeno na následujícím obrázku
|
|
|
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
0
|
 |
|
Obr. 13. Logická funkce XOR v rovině
|
Musí být tedy současně splněny následující předpoklady:
|
|
|
|
|
|
|
|
|
|
|
Pokud vztahy analyzujeme podrobněji, zjistíme, že:
Neuronové sítě - jednotlivý neuron (14) implikuje, že práh je kladný.
Neuronové sítě - jednotlivý neuron (14) a Neuronové sítě - jednotlivý neuron (15) implikuje, že je kladná a větší než práh.
Neuronové sítě - jednotlivý neuron (14) a Neuronové sítě - jednotlivý neuron (16) implikuje, že je kladná a větší než práh.
Může být součet dvou kladných hodnot, kdy jsou obě vetší než práh, současně menší než práh, jak vyžaduje bod Neuronové sítě - jednotlivý neuron (17)? Je zřejmé, že tomu tak být nemůže. Předpoklady pro realizaci funkce XOR jednotlivým neuronem tedy nemůžou být splněny a logická funkce XOR nemůže být jednotlivým neuronem realizována.




