Aktivní dynamika

Aktivní dynamika Boltzmannova stroje je opět analogická s Hopfieldovou sítí. V procesu aktivní dynamiky je opět (náhodně) zvolen v diskrétním kroku jeden z neuronů a je provedeno vyhodnocení jeho reálného vnitřního potenciálu  v souladu s (3).

(15)

Změna stavu neuronu ale nezávisí jen na hodnotě tohoto potenciálu a tedy v případě binárních neuronů jeho porovnání s nulou, změna stavu je určena stochasticky a neuron je aktivní/1, respektive pasivní/0 s pravděpodobnostmi

(16)

respektive

(17)

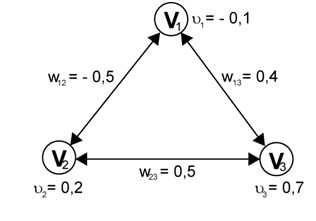
Předpokládejme síť dle obrázku Sítě se vzájemnými vazbami 8. V závislosti na teplotě T se mění pravděpodobnosti přechodů sítě mezi stavy. Zaměřme se na příklad na pravděpodobnost přechodu ze stavu 011 do dalších stavů, tabulka (3).

Obr. 8. Příklad sítě

Pro dostáváme Hopfieldovu síť s deterministickým chováním. S rostoucí teplotou roste pravděpodobnost výskytu sítě ve stavech, který by nebyl v Hopfieldově síti vůbec dosažitelný.

Proces aktivní dynamiky sítě, kdy se pracuje s hodnotou teploty se nazývá simulované žíhání. Aktivita sítě probíhá tak, že nejprve nastavíme vysokou teplotu Při vysoké teplotě se jednotlivé neurony a tedy i síť chová velmi nedeterministicky a přechází spíše náhodně mezi jednotlivými stavy. Po nějaké době aktivity sítě dojde k ustálení stavu sítě. Poté o něco snížíme teplotu a proces se opakuje. Takto postupujeme až do hodnoty včetně. Stochastické chování neuronů umožňuje s vyšší pravděpodobností překonat lokální minima energetické funkce, která mohou představovat falešné atraktory. Pro Hopfieldovu síť bylo na rozdíl od Boltzmannova stroje uváznutí v lokálním minimu konečné. Uvedený postup zajišťuje, že s vyšší pravděpodobností dosáhneme globálního minima energetické funkce a tedy skončíme v požadovaném atraktoru. Chování Boltzmannova stroje je tedy v tomto ohledu výhodnější, než chování Hopfieldovy sítě.