Stav Hopfieldovy sítě

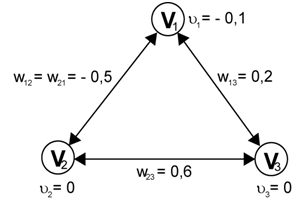
Příklad Hopfieldovy sítě se třemi uzly je uveden na následujícím obrázku. Symetrické váhy jsou označeny znakem pevné (nepodléhají adaptaci) prahy neuronů a výstupy, tedy stavy neuronů

Obr. 2. Hopfieldova síť se třemi uzly

Výstup jednotlivého -tého neuronu je definován v souladu s dříve zavedenou definicí jednotlivého neuronu jako

(3)

kde  představuje explicitní práh a aktivační výstupní funkce  má bipolární nebo binární charakter.

Variantu, kdy je aktivační výstupní funkce definována jako spojitá, například sigmoidální funkce,

(4)

nazýváme spojitou Hopfieldovou sítí, narozdíl od její diskrétní realizace s binárními či bipolárními neurony.

Hopfieldova síť s  neurony je v každém diskrétním okamžiku charakterizována vektorem výstupů jednotlivých neuronů.  Výstup každého -tého neuronu také označujeme za stav neuronu Stav sítě je pak dán vektorem o prvcích, kde každý prvek představuje stav jednoho z neuronů. Zvláštní význam má pak stav sítě v ustáleném stavu, kdy tento stav sítě představuje ukončení aktivní dynamiky sítě a tedy hledaný atraktor.