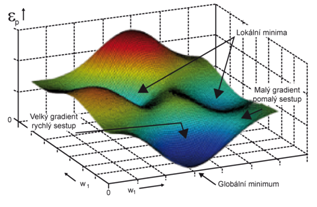
Adaptační algoritmus, například zde uvedený BP algoritmus, provádí minimalizaci chybové funkce, kde hledá gradientní metodou minimum na chybové hyperploše. Na každou váhu sítě můžeme v optimalizačním procesu pohlížet jako na jednu dimenzi n-dimenzionálního chybového prostoru. Pro dvě váhy může mít tato hyperplocha podobu jako na obrázku, kde na vodorovných osách jsou hodnoty vah a na ose svislé pak velikost chybové funkce, která je funkcí vah. Úkolem adaptačního procesu je nalézt ideálněglobální minimum. Nicméně existuje zde i riziko uváznutí v minimech lokálních.

Obr. 16. Minimalizace chybové funkce při adaptaci

Riziko uváznutí v lokálním minimu lze omezit volbou počátečních parametrů a trénovací množiny a samozřejmě i modifikací adaptačního algoritmu.

Počáteční inicializace vah neuronů

Počáteční inicializace vah definuje bod na chybové ploše, odkud při hledání minima algoritmus vychází. Pokud by byl výchozí bod počátečním nastavením vah definován na svážnici směřující k lokálnímu minimu, ze zřejmé, že globální minimum chybové funkce nalezeno nebude a minimalizace skončí v minimu lokálním. Správnou počáteční inicializaci bohužel nejsme prakticky schopni odhadnout, proto se pro počáteční inicializaci vah sítě používají náhodná čísla a v případě neúspěchu (nenalezení dostatečně přesné funkce sítě v definovaném čase nebo počtu kroků) se inicializace opakuje.

Volba rychlostní konstanty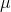

Rychlostní konstanta definuje velikost kroku, se kterým se algoritmus pohybuje po chybové ploše. Jeho výběr rovněž není jednoznačný, neboť příliš velký krok může vést k nekontrolovanému pohybu po ploše a v důsledku k nenalezení minima, malý krok naopak sice bezpečně směřuje k nejbližšímu minimu, ale konvergence algoritmu může být velmi pomalá. Kompromisní řešení představuje postupné snižování velikosti kroku během minimalizačního procesu.

Složitost chybové funkce

Tvar plochy chybové funkce závisí samozřejmě nejen na parametrech sítě (váhy, přenosové funkce) ale i na vstupních vektorech. Pokud je plocha příliš členitá s velkým množstvím lokálních minim je činnost minimalizačního algoritmu velmi ztížena. Proto jsou vstupy sítě často předzpracovávány. Cílem předzpracování je zmenšit vstupní dimenzi vektorů a zejména pak potlačit nepodstatné vlastnosti vstupních vektorů a zdůraznit vlastnosti podstatné. Eliminace nepodstatných vlastností vstupů omezuje výskyt lokálních minim v ploše chybové funkce a zjednodušuje její tvar. Bohužel o podstatnosti či nepodstatnosti některých vlastností vstupů často nejsme schopni rozhodnout jinak než intuitivně.

Způsob předkládání vstupů trénovací množiny

Je výhodné předkládat vstupy z trénovací množiny síti náhodně. Pak je i směr dalšího pohybu po chybové plošenáhodný a v důsledku umožňuje prověření širší oblasti chybové plochy.

Modifikace algoritmu BP

Modifikace algoritmu BP má za úkol omezit riziko uváznutí v lokálním minimu. Modifikace algoritmu BP spočívá v zavedení setrvačnosti do adaptačního procesu, kde zpočátku volíme blízké 1 a jeho hodnotu v průběhu adaptace zmenšujeme k nule. V případě zvýšení chyby je doporučeno setrvačnost vypustit.

Vztah Neuronové sítě - Perceptrony (12) zjednodušíme na

(32)

Zavedení setrvačnosti do vztahu znamená

(33)

Pro se pak algoritmus chová jako čistý BP algoritmus.