Metoda prohledávání do šířky, Breadth-first search (BFS)

Popis

Spolu s metodou prohledávání do hloubky základní algoritmus prohledávání stavového prostoru. Algoritmus BFS prohledává strom uzlů postupně po jednotlivých úrovních a další úroveň stromu je prohledávána až po prohledání všech uzlů úrovně předcházející.

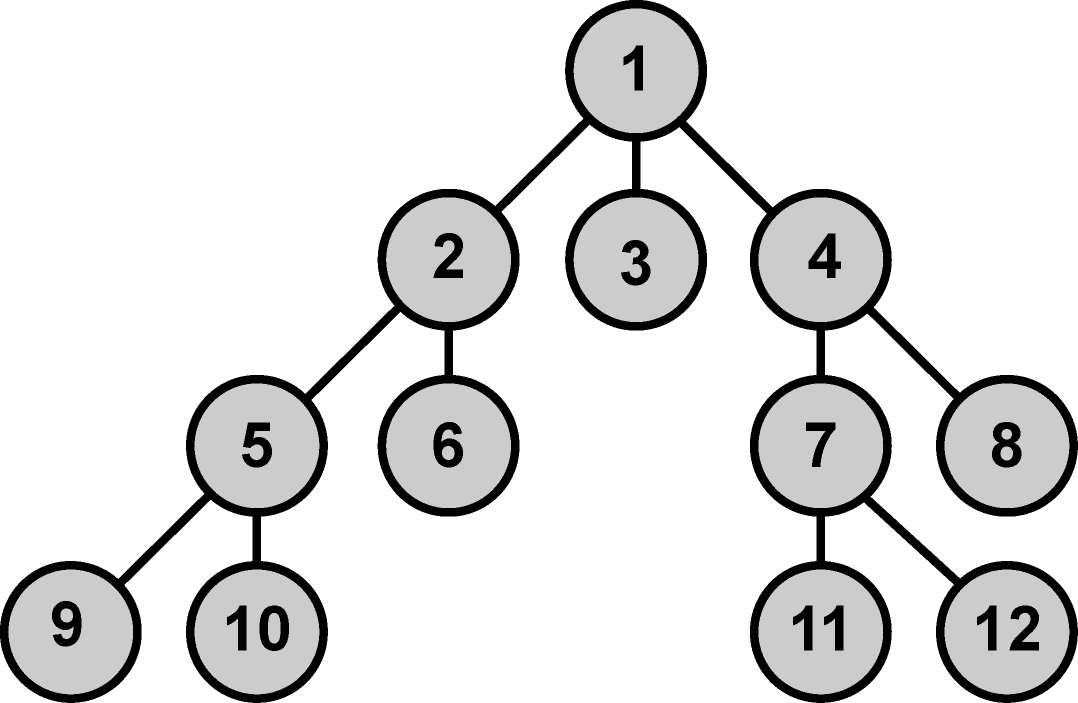Obr. 6. Prohledávací strom - příklad.

Začátek generování cesty algoritmu BFS lze pro předcházející graf zkráceně demonstrovat následujícím zápisem:

[ (1)]  -> [ (2,1) (3,1) (4,1)]  -> [ (3,1) (4,1) (5,2,1) (6,2,1)] -> [ (4,1) (5,2,1) (6,2,1)] -> [(5,2,1) (6,2,1)(7,4,1)(8,4,1)] -> …

Podoba množin OPEN(stavy k prozkoumání) a CLOSE (již prozkoumané stavy) procházených stavů bude pro tuto sekvenci následující:

OPEN[1], CLOSE[]  -> OPEN[2, 3, 4], CLOSE[1]  -> OPEN[3, 4, 5, 6 ], CLOSE[1, 2 ]->OPEN[4, 5, 6], CLOSE[1, 2, 3] ->OPEN[5, 6, 7, 8], CLOSE[1, 2, 3, 4] -> …

Generování této cesty odpovídá principu datové struktury fronty FIFO (first in, first out), kdy je vždy vybrán první, nejlevější uzel z fronty (množiny) OPEN, ten je prověřen a v případě, že nepatří mezí cílové stavy je expandován. Nově vygenerované uzly jsou zařazeny na konec fronty reprezentované množinou OPEN. Algoritmus pracuje tak dlouho, dokud nenarazí na první cílový stav, nebo dokud nevyčerpá celý stavový prostor – množina OPEN je prázdná.

Algoritmus:

1. Inicializuj množiny OPEN=[], CLOSE=[].
2. Vlož počáteční stav do OPEN.
3. Pokud je množina OPEN prázdná, ukonči algoritmus, řešení neexistuje. Jinak pokračuj dalším bodem.
4. Vyjmi první stav zleva z množiny OPEN a prověř, zda se nejedná o cílový stav. Pokud ano, máme řešení a algoritmus končí. V opačném případě vyjmutý stav drž v paměti a pokračuj dalším bodem.
5. Zapiš vyjmutý stav do CLOSE.
6. Prověř, expanduj vyjmutý stav generuj jeho následníky, další stavy.
7. Vlož všechny následníky stavu kteří nejsou v množině CLOSE na konec množiny OPEN.
8. Pokračuj bodem 3.

Vlastnosti algoritmu

Algoritmus je úplný pro konečný faktor větvení Je také optimální z pohledu délky cesty.

Časová složitost algoritmu je exponenciální, kdy počet navštívených uzlů pro cíl v hloubce můžeme pro faktor větvení vyjádřit jako:

(3)

Nejprve procházíme uzly všech úrovní předcházející úrovni, ve které se nachází cíl. To odpovídá první součtové části výrazu Pokud je cíl ve hloubce a navíc v pesimistickém případě na konci této úrovně, pak musíme ještě prověřit všechny vrstvy na úrovni, kde se cíl nachází a to včetně jeho samotného – odpovídá hodnotě uzlů ve výrazu. Navíc ale musíme pro všechny uzly v této vrstvě, mimo stavu cílového, aplikovat dle algoritmu BFS operátor na všechny uzly této vrstvy. Tuto skutečnost postihuje poslední část výrazu O(BFS), tedy

Prostorová složitost je stejně jako časová exponenciální. V množině OPEN musíme udržovat všechny uzly dané úrovně stromu v hloubce kterou jsme expandovali.  Všechny již expandované uzly všech předcházejících úrovní udržujeme v množině CLOSE.  V tomto případě je tedy prostorová složit

(4)

respektive může být při použití pouze množiny OPEN nepodstatně redukována na

(5)

Výhody a nevýhody

Hlavní výhodou je v případě předpokládaného uniformního ohodnocení hran optimálnost a úplnost algoritmu (za předpokladu konečného faktoru větvení b). Za tyto výhody však algoritmus platí velkou paměťovou složitostí, je tedy pro rozsáhlé prostory prakticky obtížně použitelný, neboť může při implementaci snadno vyčerpat fyzicky dostupné paměťové zdroje počítače. Časová složitost je v porovnání s jinými algoritmy jen průměrná.