Spearmanův korelační koeficient

Zatímco první situaci na obrázku 3 lze řešit rozdělením souboru na dva a následným výpočtem korelačního koeficientu v obou podsouborech, v situaci odpovídající grafu vpravo nahoře nemá smysl Pearsonův korelační koeficient počítat vůbec, neboť ten odráží pouze lineární závislost. Rozšíření směrem k hodnocení určitých forem nelineární závislosti představuje tzv. Spearmanův korelační koeficient (Spearman rank-correlation coefficient). Jedná se o neparametrický korelační koeficient, který je robustní vůči odlehlým hodnotám a obecně odchylkám od normality, neboť stejně jako řada dalších neparametrických metod pracuje pouze s pořadími pozorovaných hodnot. Na rozdíl od Pearsonova koeficientu korelace, který popisuje lineární vztah veličin a , Spearmanův koeficient korelace popisuje, jak dobře vztah veličin a odpovídá monotónní funkci, která může být samozřejmě nelineární.

Při výpočtu opět vycházíme z realizace dvourozměrného náhodného vektoru o rozsahu , tedy dvojic pozorovaných hodnot náhodných veličin a pro subjektů. Dále definujme číslo jako pořadí hodnoty v rámci vzestupně uspořádaných hodnot , číslo jako pořadí hodnoty  v rámci vzestupně uspořádaných hodnot , čísla  a  jako průměry hodnot , respektive (tedy jako průměrná pořadí), a čísla  a  jako odpovídající směrodatné odchylky. Spearmanův korelační koeficient, označme ho , pak vypočítáme pomocí vzorce

což není nic jiného než vzorec pro výběrový Pearsonův korelační koeficient počítaný na pořadích pozorovaných hodnot. Hodnoty se pohybují stejně jako v případě koeficientu v rozmezí od -1 do 1. Hodnot kolem nuly nabývá Spearmanův korelační koeficient v případě, že pořadí hodnot a jsou náhodně zpřeházená a mezi sledovanými veličinami není žádný vztah. Naopak hodnot -1 a 1 nabývá Spearmanův korelační koeficient v případě, že jedna z veličin je monotónní funkcí druhé veličiny.

Výpočetní alternativou ke vzorci (16) je výpočet založený na diferencích pořadí pozorovaných hodnot, které definujeme jako . Hodnotu Spearmanova korelační koeficient pak odhadneme pomocí vztahu

Tento výpočet platí přesně pouze pro neopakovaná pozorování, což znamená, že je citlivý na opakující se hodnoty, které vedou k průměrování pořadí. Vyskytuje-li se mezi hodnotami , respektive , množství shodných hodnot, je vhodnější použít k výpočtu Spearmanova korelačního koeficientu definiční vztah (16).

Příklad 4. Pro srovnání s hodnotou = 0,64 vypočtenou v příkladu 1 odhadneme korelaci výšky a hmotnosti studentů biostatistiky také pomocí Spearmanova koeficientu korelace. Hodnoty potřebné k výpočtu jsou uvedeny v tabulce 2. Vzhledem k přítomnosti opakovaných hodnot u výšky i hmotnosti vypočteme nejprve Spearmanův korelační koeficient s použitím vzorce (16):

Dále vypočteme hodnotu i pomocí vztahu (17). V tomto případě dosadíme hodnoty z tabulky 2 následovně:

Je vidět, že v tomto případě dávají oba výpočty koeficientu velmi podobné výsledky, které odpovídají střední korelaci mezi výškou a hmotností. Oba výsledky se však liší od původně vypočtené hodnoty = 0,64. Důvodem jsou dvě pozorování odpovídající hmotnosti 90 kg, které úplně nekorespondují se zbytkem souboru (viz obrázek 1). V tomto případě, kdy máme velmi limitovanou velikost výběrového souboru, je tedy lepší dát přednost neparametrické variantě, tedy hodnotě Spearmanova koeficientu korelace.

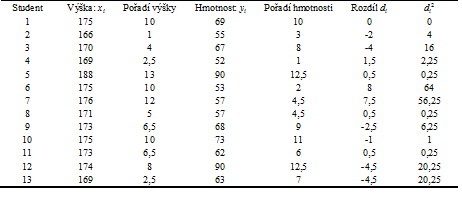
Tabulka 2: Hodnoty pro výpočet Spearmanova koeficientu korelace výšky a hmotnosti studentů.

Konstrukce intervalu spolehlivosti i test nulové hypotézy probíhá pro Spearmanův korelační koeficient stejně jako pro koeficient Pearsonův. Co se týče konstrukce intervalu spolehlivosti, výběrové rozdělení je pro výběry o velikosti alespoň 10 stejné jako výběrové rozdělení . Pro větší vzorky, kdy je velikost souboru alespoň 30, je pak možné použít pro ověření nulové hypotézy = 0 stejnou testovou statistiku jako v případě danou vztahem (13). Pro zamítnutí pak platí také stejná pravidla jako pro koeficient .