Příklad 2: Nepárový dvouvýběrový t-test

Průměrná hmotnost ovcí v čase páření byla srovnávána pro kontrolní skupinu a skupinu krmenou zvýšenou dávkou potravy. Kontrolní skupina obsahuje 30 ovcí, skupina se zvýšeným příjmem potravy pak 24 ovcí.

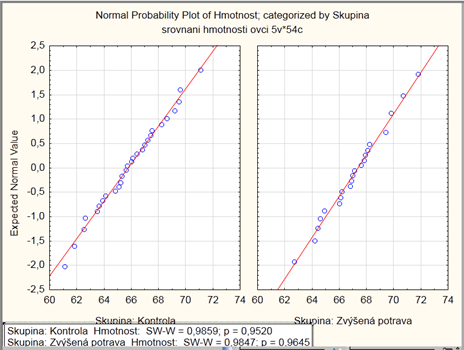
Vlastní experiment byl prováděn tak, že na začátku máme 54 ovcí (ideálně stejného plemene, stejně staré atd.), které náhodně rozdělíme do dvou skupin (náhodné rozdělování objektů  do pokusných skupin je objektem celého specializovaného odvětví statistiky nazývaného randomizace). Poté co experiment proběhne, musíme nejprve ověřit teoretický předpoklad pro využití nepárového -testu. Pro obě proměnné jsou vykresleny grafy (můžeme též spočítat základní popisnou statistiku), na kterých můžeme posoudit normalitu a homogenitu rozptylu, kromě okometrického pohledu můžeme pro ověření normality použít testy normality, pro ověření homogenity rozptylu pak F-test

Pokud platí všechny předpoklady Two sample nepárového -testu, můžeme spočítat testovou charakteristiku. Výsledné je 2,43 s  52 stupni volnosti, podle tabulek je tedy a nulovou hypotézu můžeme zamítnout. Skutečná pravděpodobnost je pak 0,018. Rozdíl mezi skupinami je 1,59 kg ve prospěch skupiny se zvýšeným příjmem.

Pro rozdíl mezi oběma soubory jsou spočítány 95% konfidenční intervaly  jako kg, což odpovídá rozsahu 0,28 až 2,91 kg. To, že konfidenční interval nezahrnuje 0 je dalším potvrzením, že mezi skupinami je významný rozdíl – jde o další způsob testování významnosti rozdílů mezi skupinami dat – nulovou hypotézu o tom, že rozdíl průměrů dvou skupin dat je roven nějaké hodnotě zamítáme v případě, kdy 95% konfidenční interval rozdílu nezahrnuje tuto hodnotu (v tomto případě 0).

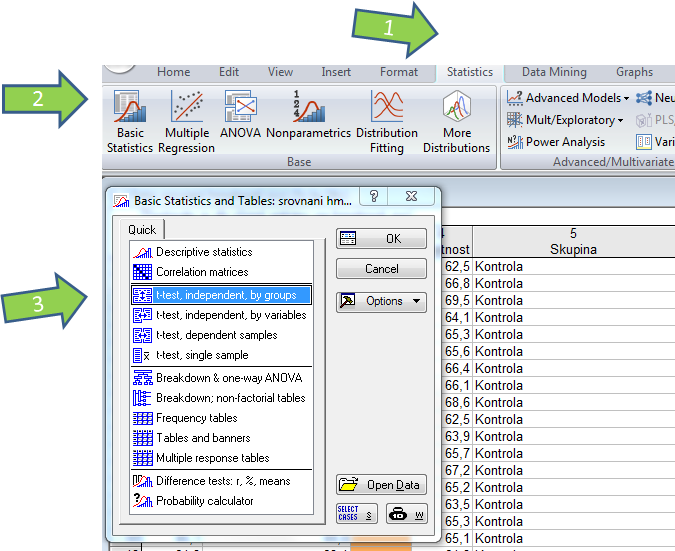
Řešení v softwaru Statistica I

Nejprve ověřte normalitu hmotnosti jednak ve skupině kontroly a ve skupině se zvýšenou potravou
V obou případech se tečky odchylují od přímky jenom málo a -hodnoty testu převyšují 0,05. Předpoklad o normálním rozložení dat v obou skupinách je oprávněný.

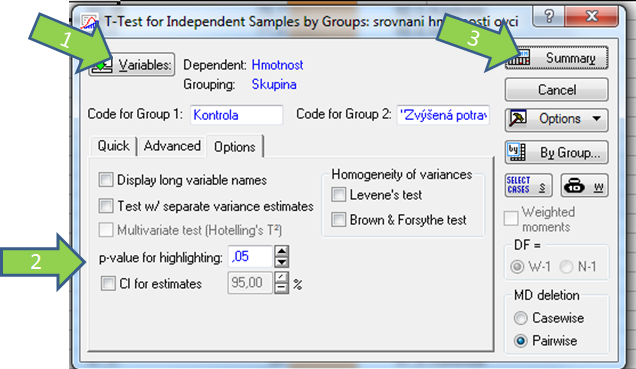
Řešení v softwaru Statistica II

V menu Statistics zvolíme Basic statistics, vybereme t-test, independent, by groups

Řešení v softwaru Statistica III

1. Zvolíme proměnné (Variables)

 

3. Kliknutím na Summary získáme výstupy

 

 

Řešení v softwaru Statistica IV

POZOR: Výstupní tabulku vyhodnocujeme zezadu!!!

 

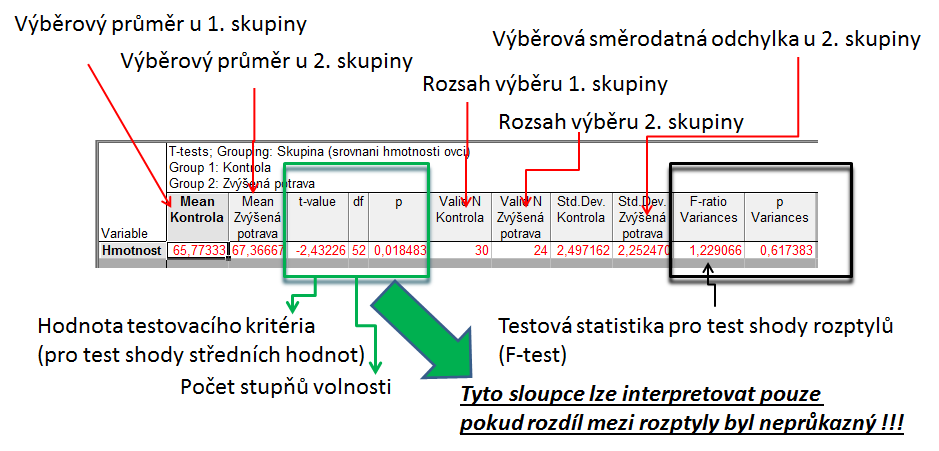Řešení v softwaru Statistica V, F-test

Pokud F-test prokázal odlišnost rozptylů, je nutné na záložce Options odškrtnout Test w/separate variance estimates (t-test se samost. odhady rozptylů)