Variabilita výběrových souborů a princip výpočtu

Abychom mohli adekvátně vysvětlit princip výpočtu analýzy rozptylu, je třeba nejprve zavést značení a předpoklady, na nichž je analýza rozptylu postavena. Obecně uvažujeme k nezávislých náhodných výběrů s rozsahy , o nichž předpokládáme, že pochází z normálního rozdělení, tedy že pro -té pozorování z -tého výběru platí . Jinými slovy předpokládáme normalitu hodnot a homogenitu rozptylů u všech náhodných výběrů (parametr odpovídající rozptylu není závislý na konkrétním výběru a je tedy stejný pro všech náhodných výběrů). Na základě výše uvedených předpokladů pak definujeme skupinové průměry pro jednotlivé výběry a celkový průměr pro všechny výběry dohromady, které uvádí tabulka 7.1.

Tabulka 7.1: Zavedení značení k analýze rozptylu.

Dále zavádíme tři odhady variability, které charakterizují pozorovaná data. První je tzv. celkový součet čtverců (total sum of squares), , který odráží celkovou variabilitu ve výběrovém souboru. Celkový součet čtverců je definován pomocí kvadrátů rozdílů pozorovaných hodnot od celkového průměru následovně:

Celkový součet čtverců je jakožto funkce pozorovaných hodnot statistikou, která má svoje rozdělení pravděpodobnosti. Lze ukázat, že za platnosti nulové hypotézy má statistika chí-kvadrát rozdělení s počtem stupňů volnosti, který se označuje jako a je roven .

Další formou variability je tzv. skupinový součet čtverců (group sum of squares), , který odráží variabilitu mezi skupinami, respektive skupinovými průměry. Jinými slovy, skupinový součet čtverců popisuje variabilitu příslušnou vlivu sledované vysvětlující proměnné. Lze ho spočítat pomocí součtu kvadrátů rozdílů výběrových průměrů od celkového průměru. Statistiku definujeme takto:

Stejně jako v případě , má i statistika chí-kvadrát rozdělení pravděpodobnosti, tentokrát ale se stupni volnosti

Třetí statistikou odrážející variabilitu pozorovaných dat je tzv. reziduální součet čtverců (residual sum of squares), , odpovídající variabilitě v rámci skupin. Spočítáme ho tak, že přes všechny výběry a pozorování sečteme kvadráty rozdílů pozorovaných hodnot od příslušných skupinových průměrů, což lze zapsat takto:

Pro statistiku lze ukázat, že platí .

Příklad 1. Tabulka 7.2 obsahuje na fiktivních datech příklad výpočtu jednotlivých součtů čtverců. V příkladu předpokládáme tři výběrové soubory, přičemž každý z nich obsahuje tři pozorované hodnoty.

Tabulka 7.2: Fiktivní datový soubor se třemi srovnávanými skupinami.

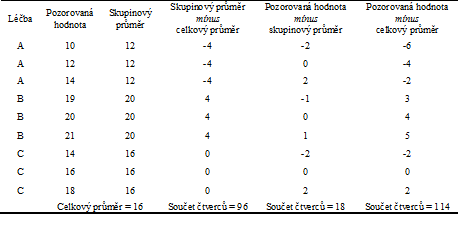V tabulce 7.2 si lze všimnout, že reziduální součet čtverců a skupinový součet čtverců dávají po sečtení dohromady celkový součet čtverců. Toto není náhoda, skutečně lze ukázat, že platí

což znamená, že celková variabilita pozorovaných hodnot se dá rozložit na variabilitu v rámci skupin a variabilitu mezi skupinami:

Stejný vztah jako (6) platí i pro stupně volnosti příslušné statistikám , a .

Výpočet analýzy rozptylu je založen na srovnání skupinového a reziduálního součtu čtverců, jinak řečeno ANOVA srovnává pozorovanou variabilitu (rozptyl hodnot) mezi výběry s pozorovanou variabilitou (rozptylem hodnot) uvnitř výběrových souborů. Za předpokladu, že hodnoty všech  srovnávaných výběrů pocházejí z normálního rozdělení se stejným rozptylem, , představuje výraz

výběrový odhad tohoto neznámého parametru. Tento podíl odpovídá průměrnému kvadrátu rozdílů pozorovaných hodnot od příslušných skupinových průměrů. Navíc, za platnosti nulové hypotézy představuje i výraz

výběrový odhad . Tento podíl odpovídá průměrnému kvadrátu rozdílů výběrových průměrů od celkového průměru. Platí-li tedy nulová hypotéza, výraz (9), vycházející z výběrových průměrů, bude zhruba stejný jako výraz (8), vycházející z pozorovaných hodnot. Naopak, neplatí-li nulová hypotéza, lze očekávat, že výraz (9) bude větší než výraz (8), neboť lze očekávat velkou variabilitu mezi výběrovými průměry (homogenita rozptylů uvnitř výběrů je základním předpokladem analýzy rozptylu). Testovou statistikou v analýze rozptylu je statistika , která je podílem výrazů (9) a (8) a která má za platnosti Fisherovo rozdělení s parametry a . Tedy

V případě, že neplatí nulová hypotéza, bude čitatel statistiky větší než její jmenovatel a výsledná hodnota statistiky tak bude větší než 1. Hranici pro zamítnutí nulové hypotézy ale opět představuje kvantil (kritická hodnota) rozdělení příslušný zvolené hladině významnosti testu . Případně nulovou hypotézu zamítneme/nezamítneme na základě srovnání výsledné -hodnoty testu se zvolenou hladinou významnosti testu . Výsledné výpočty jsou standardně zaznamenávány do tzv. tabulky analýzy rozptylu, kterou pro data z příkladu 1 představuje tabulka 7.3 (předpokládejme test na hladině významnosti = 0,05). Z této tabulky je vidět, že zamítáme nulovou hypotézu o tom, že pozorované hodnoty pocházejí z normálního rozdělení se stejnou střední hodnotou, neboť při srovnání výsledné -hodnoty testu se zvolenou hladinou významnosti platí, že 0,004 < 0,05. Pokud bychom chtěli rozhodnout o platnosti pomocí srovnání výsledné hodnoty statistiky s kritickou hodnotou, pak příslušný kvantil rozdělení je . Přitom platí 16 > 5,14, což je v souladu se závěrem pomocí výsledné -hodnoty.

Tabulka 7.3: Sumarizace výsledků analýzy rozptylu pro fiktivní data z příkladu 1.