Test hypotézy o nulové korelaci dvou náhodných veličin

I v případě malého výběrového souboru, jaký byl použit např. v příkladech 1 a 2, je logické klást si otázku, zda je či není korelace dvou sledovaných veličin nulová. Tato situace vede na testování následujících hypotéz:

Pro testování je nezbytný předpoklad realizace dvourozměrného náhodného vektoru o rozsahu n z normálního rozdělení, což znamená, že máme k dispozici náhodný vektor

Za platnosti nulové hypotézy pak má statistika

Studentovo t rozdělení pravděpodobnosti s stupni volnosti. Pro oboustrannou alternativu zamítáme nulovou hypotézu na hladině významnosti = 0,05, když hodnota testové statistiky přesáhne v absolutní hodnotě kvantil . Je třeba poznamenat, že testovou statistiku nelze použít pro testování obecné hypotézy , neboť pro r různé od nuly nemá testová statistika Studentovo rozdělení. Postup pro testování hypotézy lze najít např. v [3].

Příklad 3. Provedení testu o nulové korelaci dvou náhodných veličin opět demonstrujeme na datech výšky a hmotnosti studentů biostatistiky. Realizace testové statistiky dané vztahem (13) je následující

Srovnáme-li výslednou hodnotu testové statistiky s kvantilem Studentova rozdělení příslušným hladině významnosti = 0,05, tedy provedeme-li srovnání

zamítáme o tom, že mezi výškou a hmotností studentů biostatistiky je nulová korelace.

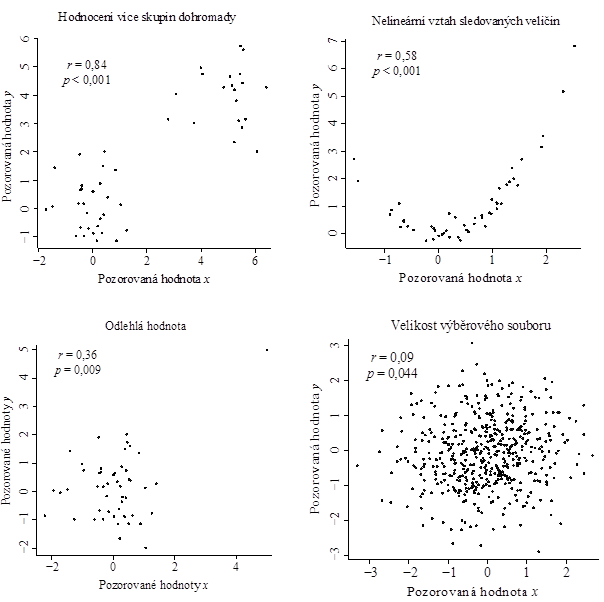
Jak bylo uvedeno výše, Pearsonův korelační koeficient kvantifikuje míru lineárního vztahu mezi náhodnými veličinami   a . Jeho výpočet je tedy naprosto nevhodný v situacích, kdy se o lineární vztah mezi a nejedná. Obrázek 3 ukazuje čtyři situace, kdy výpočet výběrového Pearsonova korelačního koeficientu nemá smysl, respektive kdy může být jeho výpočet z hlediska interpretace zavádějící. Graf vlevo nahoře znázorňuje situaci, kdy výběrový soubor obsahuje dvě skupiny subjektů s odlišnými hodnotami náhodných veličin i . Ve chvíli, kdy si tohoto nejsme vědomi, výpočet výběrového Pearsonova korelačního koeficientu indikuje silnou korelaci a (= 0,84), která je dokonce na daném souboru vysoce statisticky významná (). Tento výsledek je však statistický artefakt a ve skutečnosti není relevantní. Ideální by v tomto případě bylo soubor rozdělit a kvantifikovat korelaci v obou podsouborech zvlášť (podle obrázku je korelace a v podsouborech naopak velmi malá). Graf vpravo nahoře ukazuje situaci, kdy je mezi veličinami a nelineární vztah. Také zde je výsledný korelační koeficient ( = 0,58) relativně vysoký, statisticky významný a zároveň neodpovídá skutečnosti. Vlevo dole pak vidíme, jaký vliv má odlehlá hodnota v případě dvou nezávislých (a tedy i nekorelovaných) veličin a . Vzhledem k nezávislosti bychom čekali realizaci kolem 0, nicméně zde vidíme výsledné rovno 0,36, opět statisticky významné ( = 0,009). Konečně, graf vpravo dole ukazuje vliv velikosti výběrového souboru na statistickou významnost korelačního koeficientu. V tomto případě je korelace mezi veličinami a velmi slabá až žádná ( = 0,09), nicméně velikost výběrového souboru je tak velká ( = 500), že statistický test indikuje statisticky významný rozdíl od hodnoty 0. Toto je klasický příklad rozporu mezi statistickou a praktickou významností výsledku, kdy je nezbytné kromě statistiky do výsledné interpretace zapojit i znalost dané problematiky. Všechny čtyři problematické případy lze velmi dobře odhalit s použitím bodového grafu, který by měl být jedním z prvních kroků při hodnocení vzájemného vztahu dvou spojitých náhodných veličin.

Obr. 3: Problematické situace pro výpočet Pearsonova korelačního koeficientu.