Chí-kvadrát test dobré shody

Stejně jako Pearsonův test je i chí-kvadrát test dobré shody primárně určen pro hodnocení diskrétních náhodných veličin, kdy předpokládáme, že náhodná veličina nabývá různých hodnot , každé s pravděpodobností . Zároveň platí, že . Pokud je uvažovaný pravděpodobnostní model správný, pak by se v případě realizace náhodného výběru o rozsahu měl počet pozorování v jednotlivých variantách, tzn. pozorované četnosti , blížit hodnotě očekávaných četností . Samozřejmě platí . V případě, že náhodná veličina má předpokládané rozdělení pravděpodobnosti ( platí), má statistika chí-kvadrát rozdělení s  stupni volnosti, tedy platí

Nulovou hypotézu o shodě rozdělení veličiny s předpokládaným teoretickým rozdělením zamítáme na hladině významnosti , když realizace testové statistiky překročí příslušný kvantil chí-kvadrát rozdělení, tedy když . Často jsme v situaci, kdy chceme ověřit daný typ rozdělení, ale nemáme žádnou apriorní znalost o parametrech tohoto rozdělení. Ve chvíli, kdy nulovou hypotézou specifikujeme pouze typ rozdělení, ale ne jeho parametry, pak musíme tyto parametry odhadnout z pozorovaných hodnot. Forma testové statistiky se v takovém případě nemění, nicméně za každý takto odhadnutý parametr musíme snížit počet stupňů volnosti testové statistiky o 1.

Chí-kvadrát test dobré shody lze použít i pro spojité náhodné veličiny. Ty sice nenabývají spočetně mnoha hodnot, ale v případě, že rozdělíme obor možných hodnot náhodné veličiny do disjunktních intervalů, lze i v tomto případě test dobré shody použít pro testování shody rozdělení. Tento postup lze nejlépe demonstrovat příkladem.

Příklad 5. U pacientů s nádorem kůže sledujeme jejich věk. Pro následné použití parametrických testů chceme na hladině významnosti = 0,05 ověřit, zda lze věk těchto pacientů považovat za náhodnou veličinu s normálním rozdělením pravděpodobnosti. Nemáme však žádnou apriorní informaci o parametrech normálního rozdělení, proto potenciální hodnoty a odhadneme z dat. Na základě dat = 1536 pacientů byl vypočten věkový průměr 56,2 let s výběrovým rozptylem 182,4. Pomocí chí-kvadrát testu dobré shody tedy ověřujeme hypotézu, že věk pacientů s nádorem kůže pochází z rozdělení ( = 56,2, = 182,4). Pozorované a očekávané četnosti pacientů dle jednotlivých věkových kategorií jsou sumarizovány v tabulce 7.

Tabulka 7: Pozorované a očekávané četnosti pacientů s nádorem dle věkových kategorií.

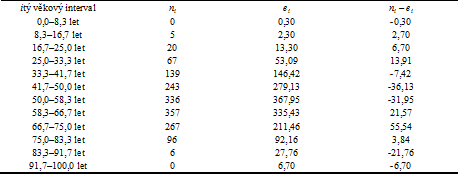Dosadíme-li četnosti z tabulky 7 do vztahu (25), získáme realizaci testové statistiky ve tvaru

Vzhledem k tomu, že bylo nutné odhadnout oba parametry normálního rozdělení z pozorovaných dat, počítáme stupně volnosti chí-kvadrát rozdělení testové statistiky pomocí výrazu . Srovnání realizace testové statistiky s kvantilem příslušným hladině významnosti = 0,05 je následující

Hodnota překročila příslušný kvantil, proto zamítáme o normalitě rozdělení věku pacientů s nádorem kůže.