
Identifikace odlehlých hodnot
Zásadní vliv odlehlých hodnot na popisné statistiky a tedy i nezbytnost jejich identifikace lze nejlépe ilustrovat příkladem.
Příklad 5. Uvažujme data z příkladu 3, v nichž zaměníme jednu hodnotu za hodnotu odlehlou (a to tak, že pouze vynecháme desetinnou čárku). Data s odlehlou hodnotou jsou dána v tabulce 2.5, odlehlá hodnota je zobrazena tučně.
Tabulka 2.5: Hodnoty cholesterolu vybrané populace mužů s odlehlou hodnotou.
|
6.2 |
7.6 |
6.3 |
9.1 |
4.2 |
5.8 |
5.65 |
6.3 |
8.6 |
6.0 |
6.2 |
|
6.7 |
4.6 |
6.25 |
6.4 |
4.04 |
6.3 |
9.1 |
6.3 |
5.2 |
64 |
5.75 |
Výpočet popisných statistik je uveden v tabulce 2.6. Srovnáme-li výsledky výpočtů na datech s a bez odlehlé hodnoty, je vidět, že odlehlá hodnota velmi výrazně ovlivňuje jak hodnotu průměru, tak výběrové směrodatné odchylky, které již vůbec neodrážejí původně naměřené hodnoty hladiny cholesterolu. Jinými slovy, průměr ovlivněný odlehlou hodnotou nelze považovat za adekvátní míru střední tendence těchto dat a výběrovou směrodatnou odchylku ovlivněnou odlehlou hodnotou nelze považovat za adekvátní míru jejich variability. Na druhou stranu, hodnota mediánu se vlivem odlehlé hodnoty nemění, neboť odlehlá hodnota nemění frekvenční střed dat.
Tabulka 2.6: Popisné statistiky vypočtené na datech s a bez odlehlé hodnoty (v mmol/l).
|
Statistika |
Výpočet na datech bez odlehlé hodnoty |
Výpočet na datech s odlehlou hodnotou |
|
Průměr: |
|
|
|
Medián: |
|
|
|
Směrodatná odchylka: |
|
|
Jak je vidět z příkladu 5, chybné hodnoty nebo také odlehlá pozorování mohou zásadním způsobem ovlivnit výsledky sumarizace dat, což může vést k mylné interpretaci a závěrům. Stejně tomu je i v případě pokročilejších statistických metod a modelů, kde je však naše schopnost odhalení odlehlé hodnoty na základě výsledků řádově horší než u jednoduché sumarizace. Je tak zřejmé, že problému odlehlých pozorování je nutné se věnovat ještě před zahájením jakýchkoliv výpočtů. Definice extrémních (odlehlých) hodnot není jednoduchá, neboť obor možných hodnot náhodné veličiny vždy závisí na konkrétním problému, který řešíme (v případě klinických dat je většinou dán rozmezím fyziologických hodnot). Někteří autoři definují odlehlou hodnotu jako hodnotu, která leží několikanásobek (tří, pěti, sedminásobek) výběrové směrodatné odchylky, respektive kvartilového rozpětí (často jedna a půl nebo třínásobek IQR), od průměru, respektive mediánu. Toto pravidlo však nelze brát striktně, neboť skutečnost, které hodnoty jsou či nejsou možné, by měl definovat hlavně zadavatel analýzy (expert na danou problematiku). Mnohem lepší je volná definice odlehlé hodnoty, která ji definuje jako netypické pozorování, které nezapadá do pravděpodobnostního chování souboru dat.
Ideálními nástroji pro identifikaci odlehlých hodnot jsou zejména výše uvedené grafy, které většinou jednoznačně odhalí problematickou hodnotu jako nezvykle vzdálenou od ostatních pozorovaných hodnot. Zajímá-li nás jedna náhodná veličina, je na místě použít histogram a krabicový graf, v případě hodnocení vztahu dvou náhodných veličin je vhodný pro identifikaci odlehlé hodnoty bodový graf. Identifikaci odlehlé hodnoty z příkladu 5 pomocí histogramu a krabicového grafu ukazuje obrázek 2.6.
Popisné statistiky jsou další pomůckou pro odhalování problematických hodnot, sumarizace minimálních a maximálních pozorovaných hodnot, případně 5% a 95% kvantilů, nám vždy jasně ukáže, v jakém rozsahu hodnot se náš soubor pohybuje. Na přítomnost či nepřítomnost odlehlých hodnot ukazuje i srovnání průměru a mediánu. Ve chvíli, kdy nám obě hodnoty vycházejí číselně podobně, můžeme usuzovat na nepřítomnost odlehlých hodnot, zatímco ve chvíli, kdy se hodnota průměru liší od hodnoty mediánu, svědčí to o přítomnosti odlehlých hodnot.
Je zřejmé, že zejména na větších datových souborech se nelze v identifikaci odlehlých hodnot obejít bez vizualizace a popisných statistik. Stejně tak se ale nelze obejít bez znalosti daného problému, která nám pomáhá se orientovat v tom, jaký je vůbec obor možných hodnot sledované náhodné veličiny.
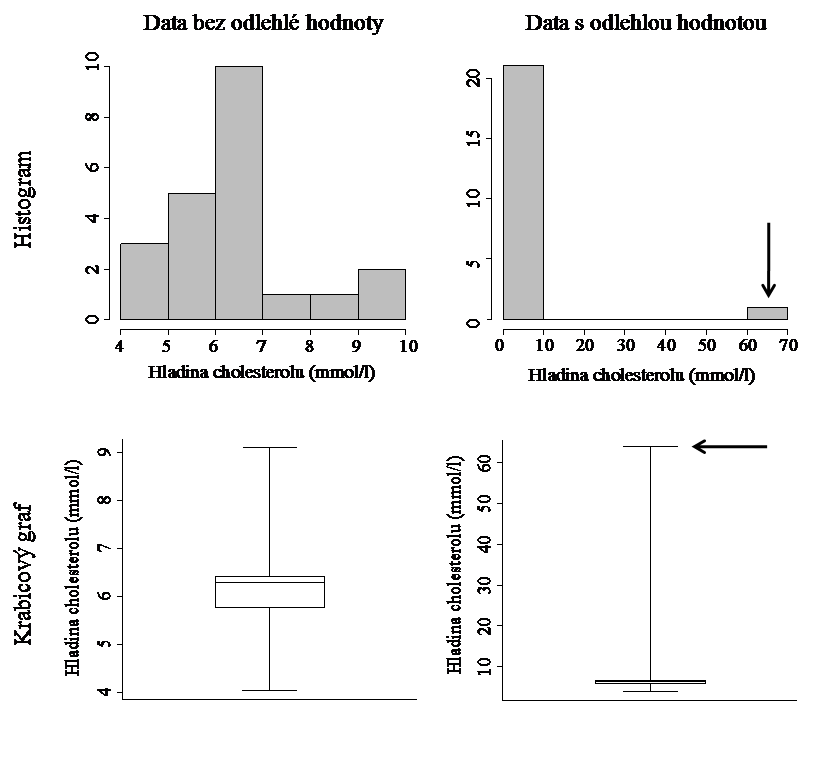 |
Obr. 2.6: Identifikace odlehlé hodnoty pomocí histogramu a krabicového grafu.




