Aplikovaná analýza klinických a biologických datAnalýza a management dat pro zdravotnické obory, Analýza klinických dat Bodové a intervalové odhady Intervalové odhady Konstrukce intervalů spolehlivosti pro parametry normálního rozdělení

Analýza a management dat pro zdravotnické obory, Analýza klinických dat |

Úvod do statistické analýzy dat pro zdravotnické obory |

Literatura |

Data, jejich popis a vizualizace |

Výstupy z výukové jednotky | Typy dat | Význam popisu a vizualizace dat |

Popis a vizualizace kvalitativních dat | Popis a vizualizace kvantitativních dat |

Identifikace odlehlých hodnot | Literatura |

Náhodná veličina, rozdělení pravděpodobnosti a reálná data |

Literatura |

Bodové a intervalové odhady |

Výstupy z výukové jednotky | Nestranné odhady | Srovnání průměru a mediánu | Teoretické pozadí intervalových odhadů |

Vlastnosti výběrového průměru | Centrální limitní věta |

Intervalové odhady |

Konstrukce intervalů spolehlivosti pro parametry normálního rozdělení | Interpretace intervalu spolehlivosti | Šířka intervalu spolehlivosti |

Literatura |

Úvod do testování hypotéz |

Spojitost testování hypotéz s intervaly spolehlivosti | Statistická a praktická významnost | Faktory ovlivňující sílu testu |

Literatura |

Testování hypotéz o kvantitativních proměnných |

Výstupy z výukové jednotky | Postup statistického testování | Testy o parametrech jednoho rozdělení |

Test o střední hodnotě při známém rozptylu (z-test pro jeden výběr) | Test o střední hodnotě při neznámém rozptylu (t-test pro jeden výběr) | Neparametrický test pro jeden výběr (Wilcoxonův test) | Test o rozdílu párových (závislých) pozorování (párový t-test) |

Testy o parametrech dvou rozdělení |

Test o rozdílu středních hodnot dvou nezávislých výběrů při stejných rozptylech (t-test pro dva | Test o shodnosti (homogenitě) rozptylů dvou nezávislých výběrů (F-test) | Neparametrický test pro dva výběry (Mannův-Whitneyho test) | Literatura |

Analýza rozptylu (ANOVA) |

Výstupy z výukové jednotky | Přínos analýzy rozptylu | Variabilita výběrových souborů a princip výpočtu | Předpoklady analýzy rozptylu a jejich ověření |

Hodnocení normality pozorovaných hodnot |

Neparametrická alternativa analýzy rozptylu – Kruskalův-Wallisův test | Literatura |

Testování hypotéz o kvalitativních proměnných |

Výstupy z výukové jednotky | Úvod | Testování hypotéz o podílech |

Interval spolehlivosti pro parametr π binomického rozdělení | Test pro podíl u jednoho výběru |

Analýza kontingenčních tabulek |

Testování nezávislosti (Pearsonův chí-kvadrát test) | Test hypotézy o symetrii – McNemarův test |

Fisherův exaktní test | Testy o rozdělení náhodné veličiny |

Chí-kvadrát test dobré shody |

Literatura |

Základy korelační analýzy |

Výstupy z výukové jednotky | Úvod | Pearsonův korelační koeficient |

Výpočet Pearsonova korelačního koeficientu | Interval spolehlivosti pro Pearsonův korelační koeficient | Test hypotézy o nulové korelaci dvou náhodných veličin |

Spearmanův korelační koeficient | Literatura |

Řešené příklady |

Aplikovaná analýza přežití | Biostatistika pro matematickou biologii |

Konstrukce intervalů spolehlivosti pro parametry normálního rozdělení

V této části kapitoly odvodíme intervaly spolehlivosti jak pro oba parametry normálního rozdělení, a .

Konstrukce 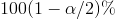intervalu spolehlivosti pro parametr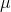

Mějme náhodný výběr z normálního rozdělení pravděpodobnosti, tedy předpokládejme, že platí . Nejprve budeme uvažovat situaci, kdy hodnotu známe. Úpravou vztahu (17) pak dostáváme:

$1 - α = P (- \frac{σ}{\sqrt{n}} z_{1 - α / 2} \leq \bar{X} - μ \leq \frac{σ}{\sqrt{n}} z_{1 - α / 2}) = P (\bar{X} - \frac{σ}{\sqrt{n}} z_{1 - α / 2} \leq μ \leq \bar{X} + \frac{σ}{\sqrt{n}} z_{1 - α / 2})$ .

(6)

Vidíme, že jsme s pomocí pravděpodobnosti a známých kvantit vypočítali dolní a horní mez, které zdola a shora omezují neznámý parametr . Správně bychom řekli, že interval spolehlivosti představuje oblast, která s pravděpodobností pokrývá neznámý parametr . interval spolehlivosti pro parametr má tedy tvar

(7)

Výraz jsme již dříve definovali jako standardní chybu výběrového průměru (viz vzorec (4)), proto interval spolehlivosti pro parametr můžeme ještě vyjádřit v alternativní formě jako

interval spolehlivosti pro .

(8)

Výše uvedené jsme odvozovali za předpokladu, že známe přesnou hodnotu parametru , což je však z praktického hlediska značně omezující (reálným příkladem však může být intervalový odhad střední hodnoty pro data měřená přístrojem s kalibrovanou a tudíž známou přesností). Ve chvíli, kdy neznáme hodnotu parametru , musíme pro konstrukci intervalu spolehlivosti použít jinou statistiku než , s jiným rozdělením pravděpodobnosti. Logické by bylo místo směrodatné odchylky, , použít výběrovou směrodatnou odchylku, , nicméně tato náhrada není úplně jednoduchá, nejedná se o pouhé dosazení za . Pomůžeme si vztahem, který definuje statistiku se Studentovým rozdělením. Statistika vypadá stejně jako statistika , jen namísto směrodatné odchylky, , obsahuje výběrovou směrodatnou odchylku, . To je přesně to, čeho jsme chtěli dosáhnout. Je však důležité si uvědomit, že statistika má jiné rozdělení pravděpodobnosti než , tedy i jinou kvantilovou funkci. Stejnými úpravami jako v případě intervalu spolehlivosti pro parametr při známém dostaneme interval spolehlivosti pro parametr při neznámém ve tvaru:

(9)

kde a jsou , respektive , kvantily Studentova rozdělení s stupni volnosti.

Příklad 2. Chceme sestrojit 95% interval spolehlivosti pro střední hodnotu systolického tlaku studentů vysokých škol. Na vzorku =100 náhodně vybraných studentů byl výběrový průměr systolického tlaku roven hodnotě 123,4 mm Hg s výběrovou směrodatnou odchylkou
= 14,0 mm Hg. Kromě těchto hodnot je třeba k výpočtu 95% intervalu spolehlivosti ještě hodnota kvantilu rozdělení příslušného hladině = 0,05 a = 99 stupňům volnosti. V tabulkách nebo příslušném software najdeme, že (99)=1,98. Dosazením do vzorce (9) získáme

(10)

což znamená, že 95% intervalem spolehlivosti pro střední hodnotu systolického tlaku studentů vysokých škol je interval (120,6 mm Hg; 126,2 mm Hg). Můžeme tedy říci, že s pravděpodobností 95 % interval (120,6 mm Hg; 126,2 mm Hg) pokrývá neznámou střední hodnotu systolického tlaku studentů vysokých škol.

Konstrukce 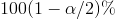intervalu spolehlivosti pro parametr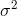

Opět předpokládejme náhodný výběr z normálního rozdělení pravděpodobnosti, tedy . Pro konstrukci intervalu spolehlivosti pro parametr použijeme vzorec využívající chí-kvadrát rozdělení, kde je procentní kvantil chí-kvadrát rozdělení s stupni volnosti:

$1 - α = P (\frac{χ_{α / 2}^{2} (n - 1)}{(n - 1) s^{2}} \leq \frac{1}{σ^{2}} \leq \frac{χ_{1 - α 2}^{2} (n - 1)}{(n - 1) s^{2}}) = P (\frac{(n - 1) s^{2}}{χ_{1 - α / 2}^{2} (n - 1)} \leq σ^{2} \leq \frac{(n - 1) s^{2}}{χ_{α / 2}^{2} (n - 1)})$ .

(11)

interval spolehlivosti pro parametr má tedy tvar

(12)

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity