Výpočet Pearsonova korelačního koeficientu

Teoretický výpočet je podmíněn znalostí konkrétního rozdělení pravděpodobnosti náhodného vektoru , což se v praxi stává velmi zřídka. Lineární vztah náhodných veličin a tak kvantifikujeme na základě výběrového souboru. Výběrový Pearsonův korelační koeficient standardně značíme a při jeho výpočtu vycházíme z realizace dvourozměrného náhodného vektoru o rozsahu , tedy dvojic pozorovaných hodnot náhodných veličin a pro první až -tou experimentální jednotku:

Výpočet výběrového Pearsonova korelačního koeficientu je pak následující:

kde a jsou výběrové průměry, a jsou výběrové směrodatné odchylky. Na obrázku 2 jsou zobrazeny realizace náhodných veličin a a k nim příslušné výběrové korelační koeficienty pro čtyři různé situace: graf vlevo nahoře odpovídá úplné lineární závislosti; graf vpravo nahoře ukazuje příklad relativně silné záporné korelace; vlevo dole pak vidíme slabě kladně korelované veličiny; vpravo dole jsou nakonec zobrazeny veličiny nekorelované.

Příklad 1 . Vypočítejme výběrový Pearsonův korelační koeficient kvantifikující korelaci mezi výškou a hmotností studentů předmětu Biostatistika v jarním semestru 2010. Pozorované hodnoty (realizace náhodného vektoru o rozsahu = 13) jsou uvedeny v tabulce 1, navíc jsou předmětem obrázku 1.

Tabulka 1: Pozorované hodnoty výšky a hmotnosti 13 studentů.

Výpočet výběrových statistik pro jednoduchost vynecháme (laskavý čtenář si je může jednoduše dopočítat na základě dat v tabulce 1), dosazením do vztahu (3) získáme následující hodnotu výběrového Pearsonova korelačního koeficientu:

Hodnota =0,64 ukazuje na silnou korelaci, kdy s vyšší výškou roste i hmotnost, což odpovídá očekávání, nicméně je třeba si uvědomit malou velikost výběrového souboru a dvě odlehlé hodnoty na obrázku 1 odpovídající hmotnosti 90 kg, které úplně nekorespondují se zbytkem souboru. Obě tyto skutečnosti ovlivňují výslednou hodnotu .

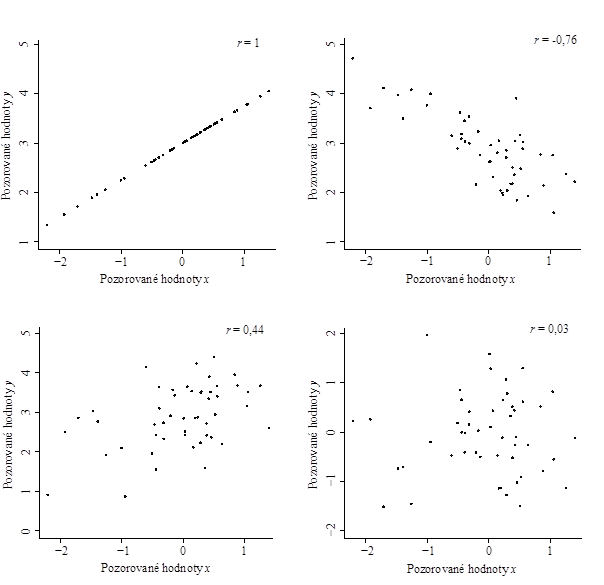Obr. 2: Ukázky realizací náhodných veličin a a vypočtené výběrové korelační koeficienty.