Definice 2.3. Systém kde je neprázdná konečná množina a je neprázdná množina relací definovaných na přičemž obě množiny společně určují vlastnosti a chování celku.

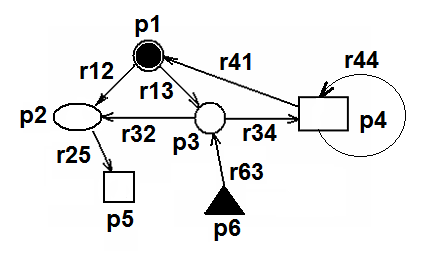
Konkrétní uspořádání prvků a vazeb systému určuje jeho vnitřní strukturu (např. obr. Kapitola počáteční 9). Kromě grafického vyjádření lze strukturu formálně vyjádřit např. čtvercovou relační maticí. Grafu podle obr. Kapitola počáteční 9 odpovídá relační matice (bez podrobnějšího popisu vlastností jednotlivých prvků a dalšího kvantitativního rozlišení jednotlivých relací) definovaná vztahem Kapitola počáteční (2).

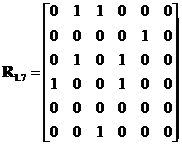(2)

Obr. 9. Příklad struktury systému

Prvky systému jsou základní součástí systému, které jsou na dané rozlišovací úrovni, resp. z hlediska dané úlohy, dále nedělitelné. Neznamená to, že by na jiné úrovni rozlišení nemohl mít prvek velice složitou strukturu.

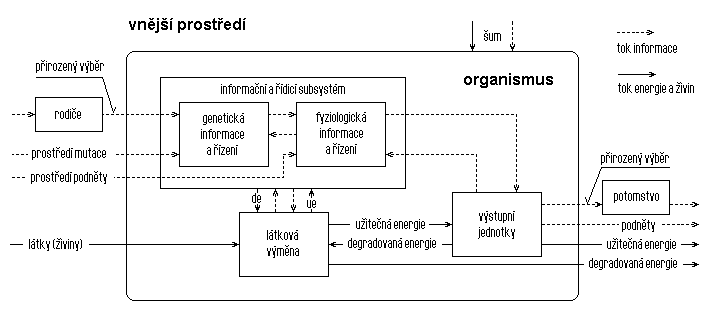
Obr. 10. Lidský organismus jako systém

V příkladu podle obr. Kapitola počáteční 10 se na dané úrovni dělí lidský organismus na tři základní elementární části (prvky) – informační a řídicí subsystém a subsystémy látkové výměny a výstupních jednotek, i když je samozřejmé, že každý z uvedených prvků (subsystémů) se reálně skládá z dalších dílčích částí, jak je naznačeno v případě informačního a řídicího subsystému, který lze členit minimálně na genetický a fyziologický subsystém. Fyziologický dále na nervovou a endokrinní soustavu, nervová na centrální a periferní, atd. Na úrovni, která je daná cíli analýzy, však zřejmě stačí základní skladba obsahující tři prvky.

Prvky popisujeme veličinami, které definují jejich stav, případně dalšími pomocnými veličinami. Veličiny, které určují stav systému, tzv. stavové veličiny jsou ty, které jednoznačně definují chování prvku i systému. Jsou to veličiny, které popisují kumulační procesy uvnitř systému. Počet stavových veličin určuje řád systému. Stav prvku, ale i systému je dán okamžitými hodnotami stavových veličin v daném časovém okamžiku. Podle vývoje hodnot stavu lze dělit systémy na statické systémy (nevykazují změnu vzhledem k nezávisle proměnné) a dynamické systémy. Chování systému je určeno vnějšími projevy systému a je důsledkem dynamiky systému, tj. schopnosti vyvolat změnu v systému, především jeho stavu.

Vazby jsou reprezentovány vztahy mezi prvky systému, případně mezi prvky systému a jeho okolí. Vazby mohou být energetické (hmotné) a informační (nehmotné). Ovšem vzhledem k tomu, co již víme o podstatě signálů, i informační vazba musí být samozřejmě reprezentována přenosem pomocí nějaké materiální veličiny. Formálně jednotlivé vazby vyjadřujeme matematickými vztahy mezi veličinami popisujícími stav prvků, přičemž závislost či nezávislost proměnných použitých ve vazebních vztazích je dána orientací vazebních relací.

Okolí systému je tvořeno prvky, které nepatří do systému, ale jsou s prvky systému svázány. Systém a jeho okolí jsou jednak objektivní skutečností, jednak i důsledkem subjektivních požadavků na obsah, formu a účel zkoumání. Např. při zkoumání stavu životního prostředí v určité lokalitě je otázka, zda zdroje znečištění zahrneme do systému, či je budeme zkoumat odděleně a jejich působení budeme považovat za vstupy systému analyzované lokality. S podobnou situací se lze setkat při teoretické analýze matematických systémů. Zahrnutí vstupů do systému analytické postupy zjednoduší.

Veličiny (vazby), které zprostředkovávají vliv okolí na systém, jsou vstupy systému a vnější projevy (vazby) systému, které reprezentují jeho vliv na okolí, příp. poskytují informavi o dějí uvnitř systému, jsou výstupy systému. Prvek systému, který má vazbu na okolí (vstupní nebo výstupní) nazýváme hraničním prvkem systému a množinu všech hraničních prvků nazýváme hranicí systému.

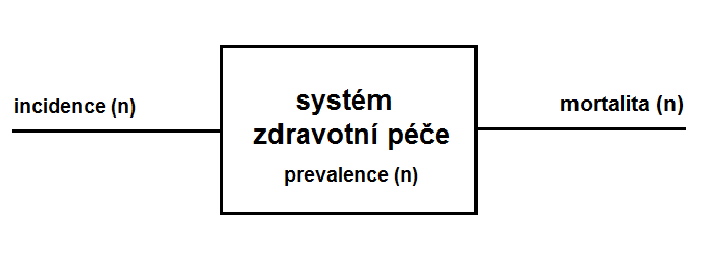
Příklad 2. 4. Incidenci a mortalitu můžeme považovat za vstup a výstup systému zdravotní péče (obr. Kapitola počáteční 11). Vzájemný vztah mezi mortalitou a incidencí formálně charakterizuje vlastnosti péče o pacienty – staticky menší mortalita při stejné incidenci znamená kvalitnější léčbu a naopak, dynamicky změny incidence se prostřednictvím léčebné péče odrážejí ve změnách mortality. Stav systému zdravotní péče je v relaci mezi oběma epidemiologickými veličinami charakterizován tzv. prevalencí, tj. okamžitým absolutním či relativním počtem pacientů s daným onemocněním. Analýzou vzájemných vztahů mezi uvedenými veličinami můžeme proto charakterizovat vlastnosti zdravotní péče a její kvalitu.

Obr. 11. Systémový pohled na epidemiologické veličiny

Ve vztahu k okolí rozeznáváme systémy otevřené a uzavřené (konzervativní). Otevřený (neautonomní) systém je takový, u něhož dochází k energetické či informační výměně s jeho okolím. Uzavřený (konzervativní, autonomní) systém je naopak od svého okolí izolován. Z praktického hlediska, abychom v případě jeho analýzy dokázali zjistit (změřit) jeho okamžitý stav, připouštíme existenci výstupních informačních vazeb.

To, zda můžeme okolí do daného systému zahrnout či nikoliv, řeší tzv. podmínka separability systému. Systém je separabilní, jestliže jeho výstupy zpětně vlivem prostředí podstatně neovlivňují vstupy.

Důležitou vlastností systému je jeho stabilita⁵. Obecně ji můžeme definovat jako schopnost systému udržovat si při změně vstupů a stavů svých prvků nezměněnou vnější formu (chování) i navzdory třeba i velice bouřlivým procesům probíhajícím uvnitř systému nebo jako schopnost systému vrátit se do původního stavu po nepříliš velkém vychýlení.

Máme-li se systémy vhodně pracovat, tj. analyzovat jejich vlastnosti, resp. syntetizovat (navrhovat jejich strukturu na základě určitých požadavků), je potřeba, podobně jako v případě veličn/signálů, umět vytvořit jejich vhodný matematický popis/model. Definice na začátku této kapitoly je určitě pěkně abstraktní, nikoliv dostatečně užitečná pro praktické úlohy. Mohli bychom se samozřejmě již zde zabývat další konkretizací uvedené definice pro konkrétní situace, nechme to ale na později uvedené, specifičtěji zaměřené lekce. Zde pouze uveďme, že matematické prostředky pro popis systémů se mohou lišit podle:

typu časové základny (spojitá, diskrétní, na čase nezávislá);
formálně i charakteru proměnných, se kterými systém pracuje (spojité, diskrétní, logické, nominální, ordinální) – z hlediska obsahu tohoto textu se v dalším budeme zabývat pouze kvantitativními proměnnými, přičemž není podstatných rozdílů mezi zpracováním proměnných se spojitým či diskrétním funkčním oborem;
vztahu k okolí (autonomní, neautonomní);
proměnnosti parametrů⁶(lineární, nelineární, časově proměnné);
vztahu k minulosti (bez paměti, s pamětí);
determinovanosti proměnných a parametrů (deterministické, nedeterministické – náhodné, fuzzy, …);
požadavků na znalost vnitřní struktury systému (vnější, resp. vstupní/výstupní popis, stavový popis).

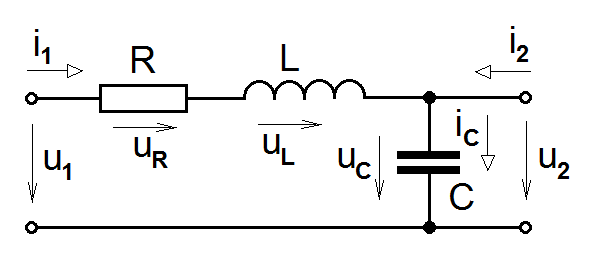
Příklad 2.5. Elektrický obvod, jehož schéma je uvedeno na obr. Kapitola počáteční 12, lze považovat (s použitím elektromechanických ekvivalencí) za fyzikální model cévního segmentu. Odpor vyjadřuje síly, kterými cévní stěny a viskozita krve působí proti pohybu krve, cívka (induktor) s indukčností reprezentuje setrvačnost krevní hmoty a kondenzátor, jako akumulační prvek elektrického náboje, nahrazuje objemovou kapacitu cévy s tím, že kapacita v podstatě vyjadřuje objemovou roztažnost (komplianci) cévy: – změna objemu cévy vyvolaná změnou krevního tlaku. Uvedená napětí ve schématu vyjadřují tlakové poměry v dané cévě, proudy i_p průtok krve cévou. Tento systém má tři prvky – odpor, cívku, kondenzátor, jejichž vlastnosti popisují parametry a a okamžitý stav každého z uvedených tří prvků je vyjádřen okamžitými hodnotami napětí a proudu těmito prvky – a (všechny tyto uvedené veličiny jsou samozřejmě funkcemi času, jehož definiční interval tvoří celá reálná osa, tzn. že všechny veličiny jsou definovány ve spojitém čase). Kontakt na okolí je vyjádřen prostřednictvím vstupního napětí a proudu (krevního tlaku na začátku cévy a průtoku krve do ní z předcházejícího segmentu) a výstupního napětí a proudu (krevního tlaku na konci segmentu a průtoku krve ven; orientace proudové šipky na výstupu segmentu je pouze formální, v případě očekávaného výtoku krve z cévy ven bude mít vypočítaná hodnota proudu v tomto případě záporné znaménko).

Obr. 12. Pasivní sériový RLC obvod jako elektrický model cévního segmentu

Matematickým modelem vazeb mezi jednotlivými prvky a veličinami, které je popisují, mohou být následujícími vztahy:

pro napětí a proud odporem platí Ohmův⁷ zákon

(3)

pro proud cívkou a indukované napětí je

(4)

pro proud a napětí na kondenzátoru (srvn. definici stažlivosti, resp. kompliance)

(5)

Dále platí 1. Kirchhoffův⁸ zákon (algebraický součet proudů v uzlu je roven nule), proto dle formalizmů uvedených v schématu

(6)

a 2. Kirchhoffův zákon (algebraický součet napětí ve smyčce je roven nule), je

(7)

Protože kumulační charakter mají dle definičních vztahů Kapitola počáteční (4) a Kapitola počáteční (5) proud cívkou a napětí na kondenzátoru budeme je považovat za stavové veličiny (jak později uvidíme, opravdu lze z jejich hodnot spočítat hodnoty všech ostatních zde uvedených veličin). Protože počet stavových veličin určuje řád systému, je analyzovaný systém 2. řádu.

¹ systém (řec. σύστημα) - složené, v celek seskupené), soustava - souhrn prvků, sdružený vzájemnými vazbami do smysluplného celku, který se navenek projevuje určitou formou chování. Původně slovo vytvořeno složením předpony σύν- dohromady a základu ϊστημι znamenajícím stát, postavit se, vydržet, stanovit, postavení. Ve významu „souhrn souvisejících principů, skutečností, resp. myšlenek” je pojem systém zmíněn již v 1. pol. 17. stol., v souvislosti s živými organismy – „tělo jako organizovaný souhrn vitálních procesů” byl použit na konci 17. století.

² Ludwig von Bertalanffy((*1901, Vídeň, + 1972 Buffalo, NY, USA), rakouský posléze ve Spojených státech žijící biolog a filosof, jeden z otců zakladatelů obecné teorie systémů.

³ Russell Lincoln Ackoff (*1919, Philadephia, PA, USA, + 2009 Paoli, PA, USA), ameriský teoretik, zabýval se problematikou a teorií operačního výzkumu a systémového myšlení.

⁴ George Jiří Klír (*1932 Praha) do roku 2007 působící na Binghamton University, NY, USA, česko-americký informatik zabývající mnoha teoretickými disciplínami informatiky, především modelováním a simulací systémů, architekturou počítačů, diskrétní matematikou, teorií fuzzy množin a problematikou soft-computing.

⁵ stabilita (lat. stabilitas, ze stabilis - stálý, ustálený, pevný vytrvalý) - pevnost, vytrvalost, stálost, , ... .

⁶ parametr - slovo vycházející z řečtiny spojením předpony παρα- s významem kromě, mimo, při a slovního kmene μητρών – míra. Původně používané v geometrii, ve 20. letech minulého století se začátky systémové teorie získalo význam „měřitelný faktor, umožňující definovat daný systém“, případně „hranice“ či „limit” tak, jak tento pojem vnímáme v současnosti. Tedy, parametry, na rozdíl od proměnných, které slouží k popisu stavu prvků, popisují základní vlastnosti či charakteristiky prvků a vazeb systému.

⁷ Georg Simon Ohm (*1789, Erlangen, Bavorsko; +1854,Mnichov) - německý fyzik; jeden ze základních zákonů nejen elektrotechniky, definující vztah mezi napětím a proudem v elektrickém obvodu zformuloval tak jednoduše, že ho německá vědecká komunita té doby naprosto nebrala vážně a vzala ho na vědomí, až když ho v roce 1841 britská Královská společnost vyznamenala za výsledky jeho vědecké práce.

⁸Gustav Robert Kirchhoff (*1824, Königsberg, Prusko, nyní Kaliningrad, Rusko; +1887, Berlín) - německý fyzik, který se zabýval především elektřinou a spektroskopií. Jeho učitelem byl Carl Friedrich Gauss.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity