2.2 Periodické posloupnosti

Diskrétní posloupnost je periodická s periodou právě když platí

(4)

ve zkráceném tvaru argumentu

(5)

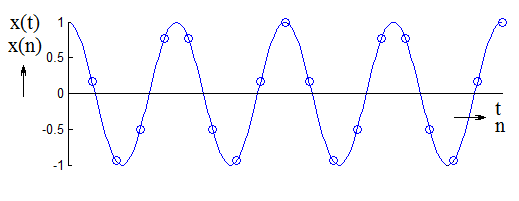
Vzhledem k tomu, že periodicita diskrétních posloupností je vázána na celočíselný násobek vzorkovací periody, je logické, že vzorkovaná spojitá periodická funkce s periodou je reprezentována periodickou diskrétní posloupností pouze tehdy, je-li perioda právě rovna celočíselnému -násobku vzorkovací periody, tj. platí Pokud by tomu tak nebylo, pak dochází k prodlužování periody diskrétní posloupnosti v závislosti na zbytku po celočíselném dělení Je-li zbytek do dělení roven prodlužuje se perioda na dvojnásobek, je-li roven pak na trojnásobek, atd. Je-li poměr obou period iracionální číslo, pak je výsledná posloupnost neperiodická.

Jako příklady periodických posloupností můžeme považovat harmonické posloupnosti popsané formulí

(6)

když a tedy nebo

(7)

Komplexní exponenciála samozřejmě stejně jako ve spojitém případě rovněž reprezentuje harmonickou, tedy i periodickou funkci, protože platí

(8)

kdy

Obr. 7. Změna periodicity funkce po vzorkování frekvencí, která neodpovídá bezezbytkovému celočíselnému podílu fvz div f.