2 Kauzalita
Kauzalita1 je vlastnost spíše systémová, v případě funkcí vyplývá až z podstaty kauzálních systémů.
Definice 2.1. Kauzální je takový systém, jehož výstup v každém časovém okamžiku závisí pouze na průběhu vstupní funkce
pro
Jinými slovy, hodnota výstupu systému v každém okamžiku závisí pouze na vstupu v daném okamžiku a jeho průběhu v minulosti, nikoliv na budoucích hodnotách vstupní funkce. Systém, který tento požadavek nesplňuje, nazýváme nekauzální, příp. anticipativní. Nebo ještě jinak, systém je kauzální, pokud se výstup systému neobjeví dříve, než je na vstup přivedena vstupní funkce. Všechny rozumné reálné systémy jsou systémy kauzální. Zpracovávané veličiny (a samozřejmě i funkce jako jejich matematické modely) zpravidla začínají v určitém referenčním okamžiku, který nazýváme počátkem časové osy. Jako kauzální funkce zprostředkovaně označujeme takové funkce, pro které platí pro
(obr. Modely veličin spojitých v čase II 4). Z toho plyne, že je možné pro kauzální funkce změnit integrační meze v definičním vztahu pro konvoluci na
|
|
(11) |
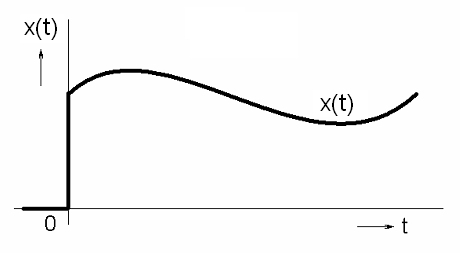
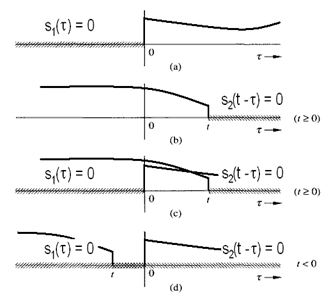
Důvody snad názorně plynou z obr. Modely veličin spojitých v čase II 5.
 |
|
Obr. 4. Kauzální funkce
|
 |
|
Obr. 5. Vzájemné pozice dvou kauzálních funkcí při výpočtu konvoluce
|
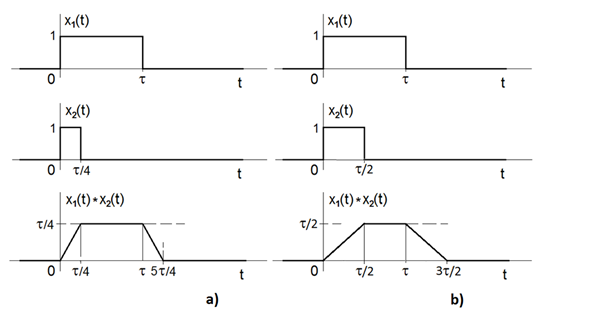
Příklad 2.2. Graficky odhadněte a vypočítejte průběh konvoluce dvou obdélníků o jednotkové výšce, když:
a) délka druhého obdélníka je čtvrtina délky prvního obdélníka;
b) délka druhého obdélníka je polovina délky prvního obdélníka;
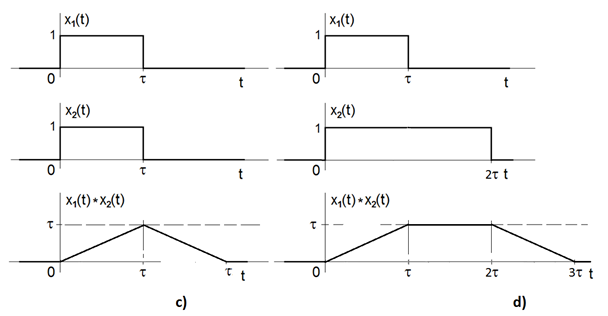
c) oba obdélníky mají tutéž délku;
d) délka druhého obdélníka je dvojnásobkem délky prvního obdélníka.
Řešení
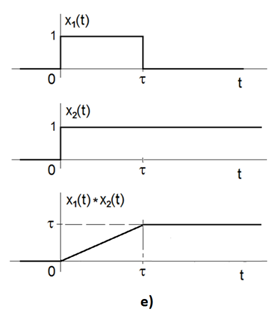
Ze všech dílčích zadání tohoto příkladu vyplývá, že čím kratší je doba trvání jedné z obou obdélníkových funkcí vstupujících do konvolučního vztahu (při zachování doby trvání druhého referenčního z obdélníků) tím ostřejší jsou přechody mezi jednotlivými úseky výsledného průběhu. V limitních případech, kterými jsou a) nekonečně krátký obdélník (ideálně jednotkový impuls) a b) nekonečně dlouhý obdélník (ideálně jednotkový skok) je výsledný tvar konvolučního výstupu:
a) tvar prvního referenčního obdélníku(podle vztahu Modely veličin spojitých v čase II (10));
b) po nástupním lineárním nárůstu po dobu trvání referenčního obdélníku
Příklad 2.3. Určete konvoluci funkcí:
a)
a
b)
c)a
Řešení.
1 kauzální (lat. causalis) – příčinný, vázaný na příčinu; kauzalita znamená vztah mezi příčinou a jejím následkem, vyjadřuje situaci, kdy jeden jev vyvolává druhý, popřípadě se oba vzájemně podporují.
