2.1 Lineární diferenciální rovnice

Diferenciální rovnice je základním způsobem popisu jakékoliv soustavy – lineární, nelineární, autonomní, neautonomní, ... . Je tedy zřejmě nejlepší tímto způsobem popisu začít.

U neautonomních systémů pracujících ve spojitém čase vyjadřuje diferenciální rovnice, jak se mění výstupní veličina a její změny v závislosti na hodnotách a jejich změnách vstupní veličiny. Pokud by byl systém autonomní, tak diferenciální rovnice popisuje pouze hodnoty a změny výstupní veličiny, přičemž tato dynamika je vyvolána pouze počátečním nastavením soustavy, tj. matematicky počátečními podmínkami řešení dané diferenciální rovnice.

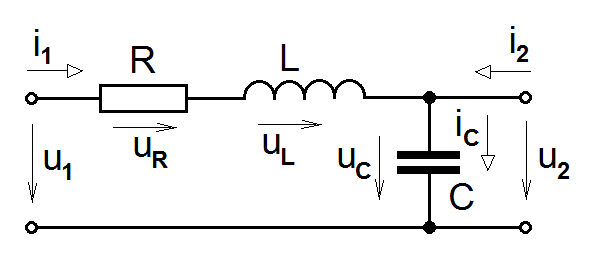
Obr. 3. Pasivní sériový RLC obvod jako elektrický model cévního segmentu

Připomeňme elektrický model cévního segmentu z příkladu v úvodní výukové jednotce Kapitola počáteční 2.5, znovu zobrazený na obr. Matematický popis systémů pracujících ve spojitém čase I 3. Z 2. Kirchhoffova zákona, uvádějícího, že součet napětí v obvodové smyčce je roven nule, je vstupní napětí obvodu rovno

(3)

A protože platí i další vztahy pro napětí na elektrickém odporu (Ohmův zákon určující napětí na reálném odporu jako součin hodnoty elektrického odporu a proudu odporem protékajícím – )

(4)

a pro proud cívkou integrální vztah

(5)

z čehož plyne, že je též

(6)

tj. napětí na cívce je úměrné změně proudu cívkou protékajícího. je tzv. indukčnost cívky, parametr v reálu určující její elektrické vlastnosti. Mechanicky v modelu cévního úseku reprezentuje hmotu proudící krve spojenou se setrvačností, matematicky to je vlastně jen konstanta úměry.

Poslední užitečný vztah, podobný vztahu Matematický popis systémů pracujících ve spojitém čase I (5), resp. Matematický popis systémů pracujících ve spojitém čase I (6) je vztah pro napětí na kondenzátoru, které je dáno kumulací (integrací) elektrického náboje, který přiteče do kondenzátoru za časovou jednotku, tj. elektrického proudu. Tedy platí

(7)

kde je kapacita kondenzátoru, parametr udávající schopnost kondenzátoru pojmout elektrický náboj (v té cévní interpretaci udávající, kolik krve je cévní segment schopný pojmout). Matematicky opět jen a jen konstanta úměry.

Za předpokladu, že je obvod tzv. na prázdno nebo bez zátěže (jinými slovy z obvodu nic neproudí – tj. platí, že ) můžeme přepsat rovnici Matematický popis systémů pracujících ve spojitém čase I (3) do tvaru

(8)

Po záměně pořadí členů na levé straně a po dosazení za proud a jeho derivaci ze vztahu mezi proudem a napětím na kondenzátoru podle Matematický popis systémů pracujících ve spojitém čase I (7) je

(9)

a protože napětí na kondenzátoru je současně i napětím mezi výstupními svorkami, tj. lze psát matematický vztah mezi výstupním a vstupním napětím napětím obvodu

(10)

a nebo možná lépe v normovaném tvaru

(11)

Počet akumulačních prvků v systému určuje řád systému a tím i jeho modelu, zde diferenciální rovnice. V řešené úloze má obvod dva akumulační prvky (), nejvyšší řád derivace výstupní proměnné je rovněž roven dvěma. Přesto, že jsme vyšli ze znalosti vnitřní struktury obvodu, odvozená diferenciální rovnice popisuje pouze vztah mezi výstupní a vstupní veličinou, bez vyjádření hodnot veličin popisujících chování jednotlivých prvků obvodu.

Obecně můžeme diferenciální rovnici popisující vlastnosti jakékoliv neautonomní lineární časově invariantní soustavy popsat ve tvaru

		(12)

kde značí výstupní veličinu, vstupní veličinu a a jsou parametry systému a a jsou nezáporná celá čísla. Chceme-li získat průběh výstupní veličiny ze znalosti průběhu vstupní veličiny a daného systému, je třeba diferenciální rovnici popisující konkrétní systém vyřešit, obecně její -násobnou integrací. Pokud je pak v řešení převažuje ideální derivační složka (ani -násobná integrace neodstraní všech derivací), jejímž důsledkem by měl např. být co do velikosti nekonečný impulz v reakci na vstupní jednotkový skok. Nekonečná hodnota je pouze teoretická možnost, reálné systémy díky různým setrvačnostem, zpožděním a jiným omezením nekonečné reakce nedosáhnou, proto reálné systémy se spojitým časem mohou být popsány diferenciální rovnicí, pro kterou musí platit

Je-li systém autonomní, tj. bez vstupu, je diferenciální rovnice homogenní, s nulovou pravou stranou. V případě výše uvedeného elektrického obvodu by to znamenalo, že na vstupu nebude žádné napětí (na začátku cévního segmentu nebude žádný krevní tlak, žádná krev nepřiteče, pouze bude odtékat) a rovnice Matematický popis systémů pracujících ve spojitém čase I (11) bude ve tvaru
 

(13)

jejíž řešení, tj. časový průběh výstupního napětí, budeme hledat pouze na základě počátečních podmínek příp. a jsou nějaké smysluplné konstanty.

Pokud parametry a nezávisejí na veličinách popisujících chování systému, tj. buď jsou konstantní, nebo maximálně závisejí ryze na čase, pak je systém lineární. Podle závislosti na čase rozlišujeme lineární systémy na časově závislé a časově nezávislé (invariantní).

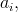
Příklad 2.1. Zdůvodněte, proč je diferenciální rovnice v obecném tvaru podle vztahu Matematický popis systémů pracujících ve spojitém čase I (12) lineární, pokud jsou parametry   konstantní.

Řešení. Způsobů, různě komplikovaných, jak to prokázat, je nepochybně více. Zde se pokusme postupovat co nejvíce analyticky. Rozložme si problém na dílčí elementy.

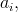
Pravá i levá strana diferenciální rovnice je dána součtem derivací různého stupně výstupní, resp. vstupní veličiny. Derivace jsou navíc váhovány parametry   které jsou dle zadání konstantní. Derivace, jak jsme si připomněli a prokázali v textu po příkladu Matematický popis systémů pracujících ve spojitém čase I 1.2, je operací lineární. Znamená to, že jak pravá, tak levá strana rovnice Matematický popis systémů pracujících ve spojitém čase I (12) obsahuje pouze součty lineárních funkcí násobených konstantami, což vlastně odpovídá obecnému tvaru principu superpozice vyjádřenému vztahem Matematický popis systémů pracujících ve spojitém čase I (2). V příkladu Matematický popis systémů pracujících ve spojitém čase I 1.2 jsme zjistili, že vadí, pokud se do funkčního vyjádření připlete absolutní člen, tedy prostá konstanta. Ta se však v rovnici Matematický popis systémů pracujících ve spojitém čase I (12) nevyskytuje ani na levé, ani na pravé straně rovnice.