Výsledek výpočtu korelačního koeficientu je skalár a je proto vhodný pro posouzení korelace dvou statických veličin. Pokud chceme zkoumat, jak se velikost korelace mění v čase u dynamických dat, je potřeba použít jinou, funkční formu popisu korelace. Takovou možnost poskytuje tzv. korelační funkce která je mírou souvztažnosti mezi hodnotami realizace náhodného procesu v okamžiku a hodnotami realizace náhodného procesu v okamžiku V souladu s definicí Pearsonova korelačního koeficientu je korelační funkce definována vztahem

(13)

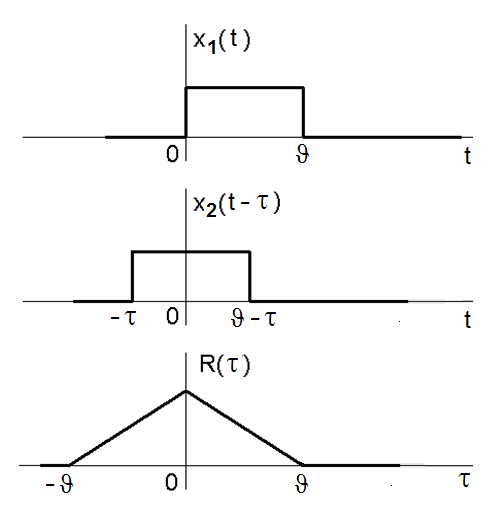
Obr. 7. Příklad průběhu korelační funkce pro dvě stejně široké obdélníkové funkce

V oblasti zpracování signálů, resp. časových řad se data častěji používají bez standardizace, tj. bez odečítání střední hodnoty a dělení směrodatnou odchylkou. V tom případě a dále za předpokladu stacionarity a ergodicity obou náhodných procesů a a jim odpovídajícím reálným realizacím a je odhad vzájemné (křížové) korelační funkce (cross-correlation function) určený z nekonečného časového intervalu závislý pouze na rozdílu obou časových okamžiků a je definován vztahem

(14)

kde je doba pozorovaného časového intervalu.

Podobné vlastnosti má tzv. kovarianční funkce, která se od korelační liší pouze tím, že hodnoty obou procesů jsou centrovány pomocí středních hodnot a daných realizací a Je definována vztahem

(15)

Pokud se zajímáme o dynamiku vztahu mezi úseky jedné realizace náhodného procesu, tu lze posoudit na základě znalosti tzv. autokorelační funkce, jejíž odhad pro ergodický proces s realizací lze pro případ se spojitým časem určit podle vztahu

(16)

resp. autokovarianční funkce definované jak

(17)

Je zřejmé, že hodnoty korelační, resp. kovarianční funkce počítané pomocí uvedených limitních výrazů jsou za předpokladu, že je hodnota integrálu v obou definičních vztazích konečná, nulové. Proto se v tom případě používají pro určení obou funkcí pouze výrazy

(18)

resp.

(19)

které ale vyjadřují pouze relativní míru vzájemnosti obou funkcí v závislosti na jejich vzájemném posunu. Totéž samozřejmě platí i pro autokorelační a autokovarianční funkci.

Nekonečné integrační meze jsou určitě teoretickou záležitostí, při zpracování reálných dat jsou k dispozici vždy jen konečné úseky zpracovávaných veličin. Pak nezbývá než průběh korelační či kovarianční funkce odhadnout z toho, co je k dispozici. Tedy pro odhad vzájemné korelační funkce dvou proměnných je

(20)

kde je konečná doba trvání známého úseku dat.

Principu korelační funkce lze použít i pro deterministické, zejména periodické funkce. I v tom případě hodnota korelační funkce definuje míru podobnosti obou funkcí v závislosti na jejich vzájemném posunutí. Pokud uvažujeme dva periodické průběhy s toutéž periodou je korelační funkce periodická s toutéž periodou. Vzájemná či křížová korelační funkce dvou periodických funkcí a o téže periodě je definována vztahem

(21)

a ekvivalentně autokorelační funkce periodické funkce je

(22)

Navzdory skutečnosti, že jsou pravé strany ve výrazech Modely veličin spojitých v čase II (20) a Modely veličin spojitých v čase II (21) stejné, díky periodičnosti funkcí a ve vztahu Modely veličin spojitých v čase II (21) představuje tento vztah výpočet skutečného průběhu korelační funkce, zatímco vztah Modely veličin spojitých v čase II (20) pouze odhad.

Autokorelační i autokovarianční funkce jsou sudé, pro všechny reálné hodnoty posunu je stejně tak jako a je rovna výkonu funkce, resp. výkonu variability dané funkce. V případě, že je zkoumaná funkce periodická, je její autokorelační (autokovarianční) funkce rovněž periodická s toutéž periodou.

Příklad 3.1. Určete průběh autokorelační funkce pro kde je jednotkový skok. Předpokládejme, že Ověřte, jaký vliv na průběh výsledné autokorelační funkce má alternace znaménka v druhém členu definičního vztahu pro výpočet autokorelace.

Řešení. Integrál

(23)

je konečný, proto budeme autokorelační funkci počítat podle vztahu

(24)

Abychom si výpočet trochu usnadnili, připomeňme si, že jednotkový skok je definován vztahem

Protože platí pro posunutý jednotkový skok

(25)

Z těchto dvou definic plyne, že pro součin obou jednotkových skoků (posunutého i neposunutého) je

(26)

To konečně znamená, že výpočet integrálu ve vztahu Modely veličin spojitých v čase II (24) může být formulován

(27)

Uvažme teď alternativu výpočtu autokorelační funkce podle vztahu

(28)

To znamená, že je

(29)

V tom případě pro součin obou jednotkových skokových funkcí (posunuté i neposunuté) je

(30)

a výpočet integrálu z Modely veličin spojitých v čase II (29) je

(31)

Oba výsledky nám na konkrétním příkladu demonstrovaly konstatování o sudosti autokorelační funkce, protože oba získané výsledky jsou stejné bez ohledu na volbu znaménka v definičním vztahu pro výpočet korelace.

Příklad 3.2. Vypočtěte průběh vzájemné korelační funkce funkcí a Ověřte, jaký vliv na průběh výsledné korelační funkce má alternace znaménka v druhém členu definičního vztahu.

Řešení. Protože argumenty obou harmonických funkcí jsou mají obě harmonické funkce tutéž periodu [časové jednotky]. Tedy

(32)

Pokud by byla korelační funkce definována pomocí vztahu

pak je

(33)

Tentokrát se oba výsledky liší ve znaménku a pro oba případy je hodnota korelační funkce pro rovna nule. V podstatě se pro daný konkrétní případ vypočtená vzájemná korelační funkce jeví jako lichá (pozor - nelze zobecnit). Pokusme se pomocí obr. Modely veličin spojitých v čase II 8 tento rozdíl alespoň zhruba interpretovat.

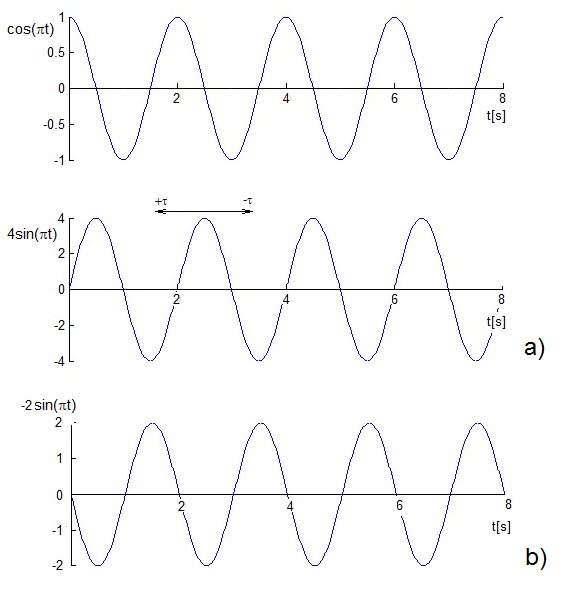Obr. 8. a) Harmonické funkce dle zadání příkladu, b) výsledná korelační funkce

Při výpočtu korelační funkce pomocí vztahu dochází při k posunu funkce sin směrem k menším hodnotám na časové ose (vlevo). To znamená, že podobnost obou křivek posunem z výchozího postavení nejdříve roste. Protože funkce s nárůstem hodnoty také nejdříve roste, odpovídá to očekávanému nárůstu hodnoty korelace.

Při výpočtu korelační funkce pomocí vztahu dochází při k posunu funkce sin směrem k větším hodnotám na časové ose (vpravo). To znamená, že podobnost obou křivek posunem z výchozího postavení nejdříve klesá. Protože funkce sin(pt) s nárůstem hodnoty od nuly nejdříve roste, odpovídá to očekávanému poklesu hodnoty korelace vyjádřené funkcí

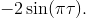
Příklad 3.3. Určete hodnotu autokorelační funkce pro a korelační funkce pro a kde je celé číslo, pro

Řešení. Funkce je periodická, autokorelační funkci proto budeme počítat podle vztahu Modely veličin spojitých v čase II (22). Je tedy

a pro bude

Pro žádanou korelační funkci bude

Protože oba získané výrazy integrujeme přes periodu funkce kde a frekvence druhé funkce je dána celočíselným násobkem frekvence první funkce, jsou oba dílčí integrály rovny nule, tedy je i

Pokusíme-li se zobecnit tyto výsledky, pak můžeme konstatovat, že hodnota korelační funkce periodické funkce s jádrovou harmonickou funkcí se stejnou periodou pro nabývá nějaké, obecně nenulové hodnoty (její velikost zatím nerozebírejme). Pokud budeme počítat hodnotu korelace mezi periodickou funkcí a jádrovou harmonickou funkcí, jejíž frekvence je rovna celočíselnému násobku frekvence dané periodické funkce, pak korelační funkce a tím i její hodnota pro je nulová.

¹V odborné literatuře se často liší definice korelační funkce ve znaménku před argumentem ve funkci v integrálu na pravé straně výrazu. Tato diference znamená, že se definice liší ve vnímání posunu druhé funkce v čase. Je-li pak výraz reprezentuje posun funkce směrem k záporným hodnotám času (viz kap. 2.4.1) a výraz posun funkce směrem ke kladným hodnotám času. Jak posléze uvidíme, z hlediska autokorelační či autokovarianční funkce, které jsou sudé, nemá volba znaménka na výsledný průběh žádný vliv, z hlediska vzájemné korelační, resp. kovarianční funkce reprezentuje volba znaménka inverzi časové osy výsledné funkce. To samozřejmě může způsobovat nedorozumění v interpretaci výsledků, proto je třeba být si vědom této skutečnosti a volby. Protože se varianta s kladným znaménkem vyskytuje častěji, dáváme v tomto textu přednost této variantě.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity