1.2 Fourierova řada

(1)

kde je úhlový kmitočet základní harmonické složky určený základní periodou rozkládané funkce a a jsou Fourierovy koeficienty dané vztahy

(2)

Protože již víme, že trigonometrické vyjádření harmonické funkce zcela jednoznačně souvisí se základním kosinovým definičním vztahem (Modely veličin spojitých v čase I (9) – Modely veličin spojitých v čase I (11)), lze využít definičního tvaru kosinové funkce pro tzv. harmonickou Fourierovu řadu

(3)

kde

(4)

a pro

(5)

(6)

a výraz nazýváme -tou harmonickou složkou funkce

Oba uvedené způsoby zápisu Fourierovy řady souvisí s tím, jak lze obecný fázově posunutý tvar harmonické funkce vyjádřit součtem kosinové a sinové složky.

Je-li sudá, tj. pak pro všechna Na rozvoji sudé funkce se tedy podílejí pouze kosinové, tj. sudé složky. Podobně, je-li lichá, tj. je pro všechna a  K rozvoji liché funkce proto přispívají pouze liché sinové složky.

Nyní si uvědomme následující skutečnost, která poskytne základní význam a porozumění podstaty uvedeného rozkladu periodické funkce pomocí Fourierovy řady. Když podrobněji pohlédneme definiční vztahy Modely veličin spojitých v čase III (2) pro koeficienty Fourierova rozvoje a připomeneme si vztahy pro vzájemnou korelaci dvou funkcí, především vztah pro korelaci dvou periodických funkcí, vidíme, že vyjadřují hodnotu korelační funkce pro nulové posunutí, tj. mezi analyzovaným průběhem a průběhem harmonických funkcí kosinus a sinus s nulovou počáteční fází a s frekvencí, která se rovná celočíselným násobkům úhlového kmitočtu základní harmonické složky dané periodou rozkládané funkce To znamená, že amplitudy harmonických složek, ze kterých se analyzovaná funkce skládá, jsou dány velikosti korelace mezi funkcí a referenčními harmonickými složkami. Aby se do výpočtu korelace nepromítal vliv dalších harmonických funkcí (s jinou frekvencí), je třeba, aby se funkce, na které daný průběh rozkládáme, tzv. bázové funkce (v případě Fourierovy řady funkce harmonické) navzájem neovlivňovaly, aby byly ortogonální nad daným intervalem, což jak jsme uvedli v předešlé kap. 1.1 Proč?, harmonické funkce s frekvencí rovnou celočíselnému násobku základní referenční frekvence splňují.

Pokud preferujeme pro vyjádření harmonického průběhu komplexní exponenciálu, lze Fourierovu řadu psát ve tvaru

(7)

kde  jsou komplexní Fourierovy koeficienty definované vztahem

(8)

a je opět úhlový kmitočet základní harmonické složky určený základní periodou T rozkládané funkce Modul komplexního Fourierova koeficientu  určuje amplitudu odpovídající harmonické složky, jeho fáze hodnotu počáteční fáze odpovídající harmonické funkce.

Pro je

(9)

což je střední hodnota (stejnosměrná složka) funkce

Pro reálné funkce je  (symbolem označujeme komplexně sdruženou hodnotu).

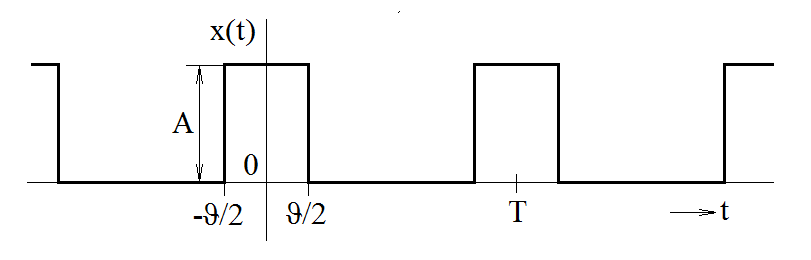
Příklad 1.1. Určeme vlastnosti jednotlivých harmonických složek, z nichž se skládá obdélníkový pulz (obr. Modely veličin spojitých v čase III 2) o základní periodě době trvání jednotlivých impulzů a výšce Nechť je první z impulzů umístěn symetricky kolem počátku časové osy.

Obr. 2. Zadání obdélníkového pulzu

Řešení. Spočítejme nejdříve hodnotu pomocného integrálu

(10)

Pro je

(11)

a pro

	(12)

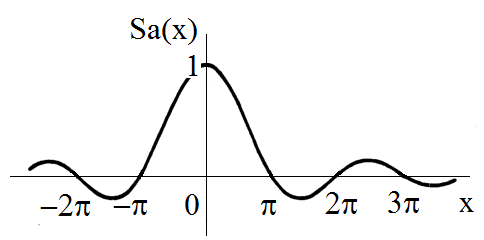
Tvar vypočítané funkce je na obr. Modely veličin spojitých v čase III 3. Funkce je primárně dána průběhem funkce je však tlumena s lineárním růstem hodnoty ve jmenovateli zlomku. Pro určení hodnoty použijeme limitu výrazu pro což lze snadno spočítat podle l’Hospitalova pravidla.

Obr. 3. Průběh funkce Sa(x) = sin(x)/x

S tímto výsledkem lze spočítat Fourierovy koeficienty zadaného obdélníkového pulzu podle následujícího postupu

	(13)

Koeficienty  tedy nabývají hodnot funkce pro diskrétní hodnoty argumentu vynásobené výrazem tj. plochou jednoho impulzu normalizovaného vztažené k době trvání periody. Protože koeficienty jsou obecně komplexní, lze jejich hodnoty vyjádřit pomocí závislostí jejich modulů a fází na frekvenci jednotlivých harmonických složek. Tyto závislosti označujeme jako amplitudové (modulové) a fázové frekvenční spektrum periodické funkce. Protože jsme vycházeli z exponenciálního tvaru Fourierovy řady, je třeba předpokládat jak kladné, tak záporné hodnoty n a tím uvažovat frekvenční složky o kladných i záporných frekvencích. Vzhledem k tomu, že hodnoty koeficientů počítáme jen pro určité kmitočty, které jsou celočíselnými násobky kmitočtu základní harmonické složky, je spektrum této funkce a všech periodických funkcí diskrétní (čarové).

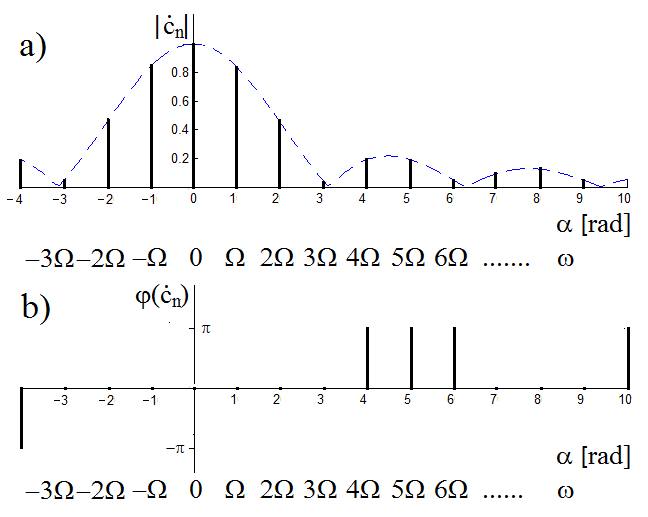
Obr. 4. a)Amplitudové (modulové) a b) fázové frekvenční spektrum obdélníkového pulzu symetrického podle počátku časové osy

Grafické znázornění hodnot modulů a fází koeficientů pro obdélníkový pulz podle zadání je na Modely veličin spojitých v čase III 4. Obě části spektra, tj. amplitudové i fázové jsou díky periodicitě analyzované funkce diskrétní, resp. čárové. To znamená, že jsou definovány pouze pro určité frekvence, které jsou rovny celočíselným násobkům základní harmonické frekvence kde je základní perioda analyzovaného veličiny. Jednotlivé amplitudové spektrální čáry nabývají hodnot právě rovných hodnotám obálkové funkce reprezentované čárkovanou čarou, která je dána formulí

Protože amplituda musí být kladná, je obálková funkce určena absolutní hodnotou. Nulové hodnoty nabývá pro argumenty funkce rovné celočíselným násobkům  tj.

a tedy pro frekvenci

Jak plyne ze vztahu Modely veličin spojitých v čase III (13), jsou hodnoty Fourierových koeficientů ryze reálné a nabývají kladných i záporných hodnot podle průběhu funkce Zobrazeno v komplexní rovině to znamená, že fáze koeficientů je nulová, pokud jsou jejich hodnoty kladné a rovny hodnotě (180°), resp. (–180°) na záporné frekvenční poloose, pokud jsou hodnoty Fourierových koeficientů záporné.

Příklad 1.2. Co se stane, když posuneme obdélníkový pulz z předešlého příkladu tak, aby nástupná hrana obdélníka byla v počátku časové osy (obr. Modely veličin spojitých v čase III 5)?

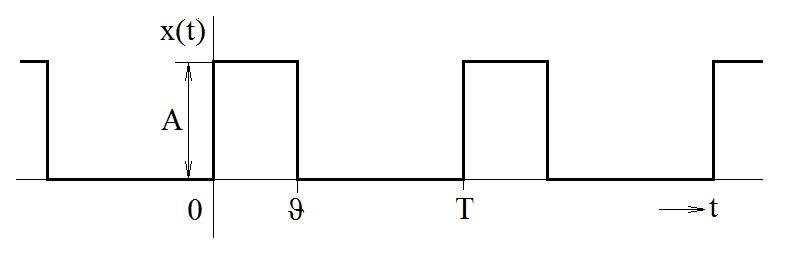Obr. 5. Zadání posunutého obdélníkového pulzu

Řešení. V tomto případě spočítáme hodnoty Fourierových koeficientů podobně jako v předešlém příkladě:

	(13)

Srovnáním výsledků příkladů Modely veličin spojitých v čase III 1.1 a Modely veličin spojitých v čase III 1.2 zjistíme, že výsledné vztahy se liší pouze v tom, že ve druhém případě výsledek násobíme ještě exponenciálním členem Co násobení tímto členem znamená? Protože komplexní exponenciála představuje komplexní číslo s jednotkovým modulem a fází znamená to, že Fourierovy koeficienty již v tomto případě nejsou ryze reálná čísla, nýbrž obecně komplexní, přičemž fáze je přímo úměrná celočíselným násobkům základní úhlové frekvence původního periodického pulzu Dosadíme-li za do výrazu pro fázi dostaneme Tedy, hodnoty modulů Fourierových koeficientů se nemění, pouze jejich fáze pro n-násobky základní harmonické frekvence nabývají hodnot (obr. Modely veličin spojitých v čase III 6).

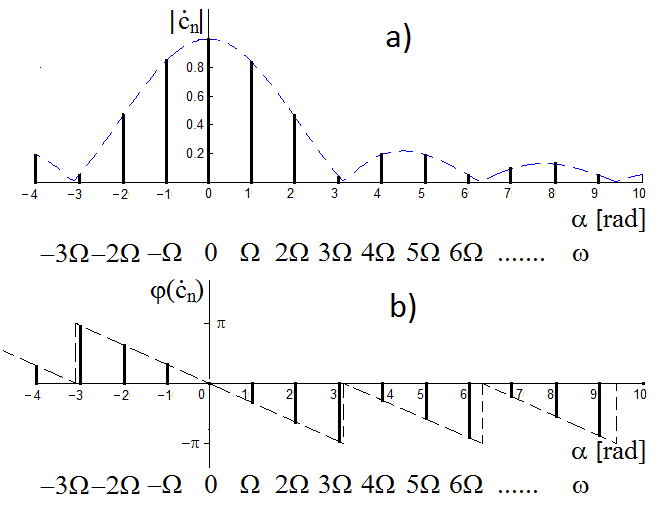Obr. 6. (a) Amplitudové (modulové) a (b) fázové frekvenční spektrum obdélníkového pulzu s nástupnou hranou v počátku časové osy