4.2 Vlastnosti zpětnovazebního zapojení

Zpětnovazební zapojení má mnohé pozitivní, pro praxi užitečné vlastnosti, jako např.:

• schopnost vhodně reprodukovat vstup (princip regulace);
• snížená citlivost poměru výstup/vstup na změny parametrů systému;
• snížený vliv nelinearit;
• snížený vliv vnějších poruch a šumu;
• širší rozsah frekvenčního pásma.

Může ale způsobit (při zavedení kladné zpětné vazby) i nepříjemné těžkosti, které vedou k možnému vzniku oscilací a nestabilitě.

Z uvedených vlastností si na příkladu demonstrujme možnost rozšíření propustného frekvenčního pásma.

Příklad 4.1. Ověřte vliv zpětné vazby na frekvenční vlastnosti zpětnovazebního systému s úplnou zápornou zpětnou vazbou podle obr. Systémové struktury 5, je-li v přímé větvi systém 1. řádu s přenosovou funkcí

(27)

Řešení. Připomeňme, že z praktických důvodů je užitečné obrazovou přenosovou funkci tohoto typu psát ve tvaru

(28)

kde je koeficient zesílení (říká kolikrát je výstupní signál větší než vstupní v celém frekvenčním pásmu) a je časová konstanta reprezentující setrvačnosti systému a která rovněž úzce souvisí s mezní frekvencí přenášeného pásma.

Frekvenční přenosová funkce zadaného systému v přímé větvi je

(29)

a frekvenční přenosová funkce výsledného zpětnovazebního systému

(30)

Ze vztahu Systémové struktury (30) je zřejmé, že si systém zachovává globální vlastnosti - opět se jedná o systém 1. řádu se setrvačností, zmenšil se ale koeficient zesílení z 1 na 0,5 a podobně se zmenšila i časová konstanta systému, opět z 1 na 0,5.

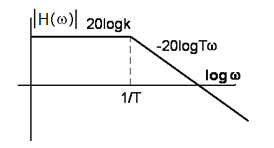
Bodeho modulová frekvenční charakteristika systému 1. řádu se setrvačností je určena vztahem

(31)

Zopakujme si rovněž, že grafické znázornění Bodeho frekvenční charakteristiky je založeno na aproximaci lomenou přímkou pro dva mezní případy:

• pro je   a tedy

(32)

• pro je   a tedy

(33)

Modulová Bodeho frekvenční charakteristika systému 1. řádu se setrvačností má proto tvar uvedený na následujícím obrázku.

Obr. 5. Modulová Bodeho charakteristika systému 1. řádu se setrvačností

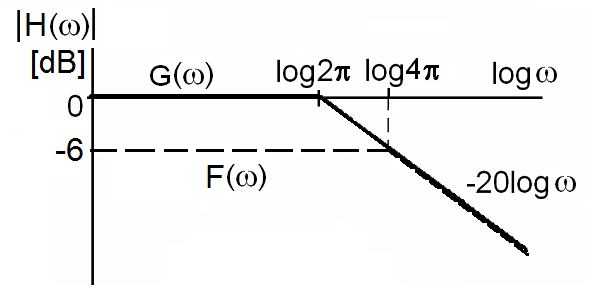
V zadaném případě má zpětnovazební zapojení v propustném pásmu poloviční zesílení, tedy nikoliv jako původní zadaná soustava, ale tj. Ve svých klesajících částech jsou frekvenční charakteristiky obou systémů popsány výrazy

		(34)

To znamená, že jejich průběh je v této části stejný. Tvar frekvenčních charakteristik obou soustav je zobrazen na následujícím obrázku.

Obr. 6. Modulová Bodeho charakteristika systému 1. řádu se setrvačností dle zadání

Frekvenční charakteristika zpětnovazebního systému má oproti původnímu dvojnásobně široké přenášené pásmo, ovšem za cenu snížení zesílení na polovinu.