3.2 Diskrétní konvoluce

Zopakujme nejdříve, že konvoluce pro dvě spojité funkce a byla definována vztahem Modely veličin spojitých v čase II (1)

Pokusíme-li se vytvořit diskrétní ekvivalent tohoto vztahu, pak i bez velkého přemýšlení lze psát

(15)

A protože konvoluce má komutativní vlastnost platí samozřejmě stejně jako ve spojitém případě i

(16)

Pro kauzální posloupnosti, tj. takové, pro které platí pro se konvoluční vztah mění Modely veličin spojitých v čase II (11) na

(17)

V reálných podmínkách při zpracování reálných dat samozřejmě nejsou posloupnosti a nekonečné, nýbrž mají konečnou délku. Předpokládejme obecně vzorků v případě posloupnosti a vzorků v případě posloupnosti Dále položme pro a analogicky pro V tom případě je

(18)

Algoritmus výpočtu konvoluce dvou konečných posloupností spočívá v součtu dílčích součinů prvků posloupnosti a v čase invertované a o n prvků směrem v kladné časové ose posunuté posloupnosti (obr. Časové řady I 10).

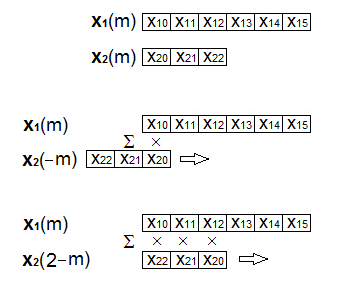Obr. 10.  Schéma výpočetního algoritmu konvoluce konečných posloupností

Příklad 3.1. Vypočtěte konvoluci posloupností a

Řešení. Pro výpočet se také občas uvádí následující výpočetní schéma:

Příklad 3.2. Podle výše uvedeného výpočetního schématu spočítejte konvoluci dvou posloupností a (obr. Časové řady I 11).

Řešení.

Výsledkem konvoluce obou posloupností je tedy posloupnost     (obr. Časové řady I 11 ).
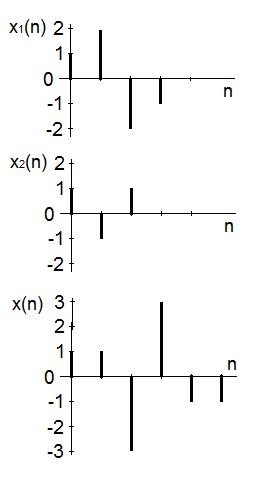	Obr. 11. Zadání a řešení příkladu

Z výpočetních schémat v předchozích příkladech je zřejmé, že na začátku, ale je tomu tak i na konci výpočtu, konvoluční suma nezahrnuje všechny dílčí součiny, jak by plnohodnotně náleželo podle délky obou posloupností – nastává jistý přechodný děj.

Tento jev by bylo možné eliminovat za předpokladu periodičnosti alespoň jedné z obou posloupností.

Předpokládejme, že délka obou posloupností je což je současně perioda posloupnosti Potom můžeme konvoluční vztah definovat jako

		(19)

Takový způsob výpočtu nazýváme kruhová konvoluce a jeho výpočetní schéma je zobrazeno na obr. Časové řady I 12.

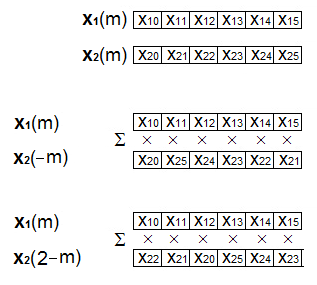Obr. 12. Výpočetní schéma kruhové konvoluce

Příklad 3.3. Vypočítejte konvoluční posloupnost pro vstupní posloupnosti

a

Řešení

Protože posloupnost je posloupnost odpovídající diskrétnímu jednotkovému impulzu, tak díky platnosti vztahů Časové řady I (11) a Časové řady I (12) je výsledná konvoluční posloupnost rovna posloupnosti

 

Příklad 3.4. Vypočítejte konvoluci posloupností

a

Řešení.

 

Příklad 3.5. Vypočítejte konvoluci posloupností

a

Řešení.

Z tohoto i předcházejícího příkladu vyplývá i platnost šířkové vlastnosti konvoluce – délka výsledné posloupnosti je rovna součtu délek obou vstupních posloupností mínus jedna.

 

Příklad 3.6. Vypočítejte kruhovou konvoluci pro vstupní posloupnosti a

Řešení. Výsledná posloupnost je                                                               

 

Příklad 3.7. Vypočítejte kruhovou konvoluci pro vstupní posloupnosti a

Řešení. Výsledná posloupnost je