Definice 1.1. Komplexní čísla jsou čísla ve tvaru kde jsou reálná čísla a je tzv. imaginární jednotka. Číslo a se nazývá reálná část (složka) komplexního čísla a reálné číslo nazýváme imaginární část (složka) komplexního čísla Platí-li nazýváme komplexní číslo ryze imaginárním.

Poznámka 1.2. V matematických textech je zvykem pro vyjádření imaginární jednotky používat písmeno i. V elektrotechnických textech, kde se problematika zpracování signálů a časových řad objevila jako první, se písmene i používá k označení jedné ze základních elektrotechnických veličin a to okamžité hodnoty elektrického proudu. Proto se v textech, zabývajících se problematikou zpracování signálů, používá k označení komplexní jednotky symbolu j. Budeme se nadále držet této konvence navzdory skutečnosti, že tyto texty jsou určeny především pro čtenáře s matematickým vzděláním, protože se domníváme, že tento zvyk usnadní případné doplňkové studium publikací o zpracování signálů a časových řad.
Výše uvedenou definici komplexního čísla tedy budeme vnímat ve tvaru

Imaginární jednotka byla zavedena a použita, aby bylo možné zvládnout řešení rovnic typu Proto pro imaginární jednotku platí mocniny

(1)

kde je celé nezáporné číslo.

Definice 1.3. Číslo s imaginární složkou s opačným znaménkem označujeme jako komplexně sdružené k číslu

Poznámka 1.4. Komplexní čísla jsou dle definice Komplexní čísla 1.1 v podstatě dána uspořádanou dvojicí reálných čísel, což vlastně vede k podobnému nahlížení, znázornění i k manipulaci jako v případě dvousložkových vektorů. Komplexní číslo (je-li zcela zřejmé, že se o komplexní číslo jedná a nelze je tudíž zaměnit s dvousložkovým vektorem) můžeme také zapsat ve tvaru

Definice 1.5. Zápis komplexního čísla po složkách ve tvaru nebo nazýváme složkový nebo kartézský tvar komplexního čísla.

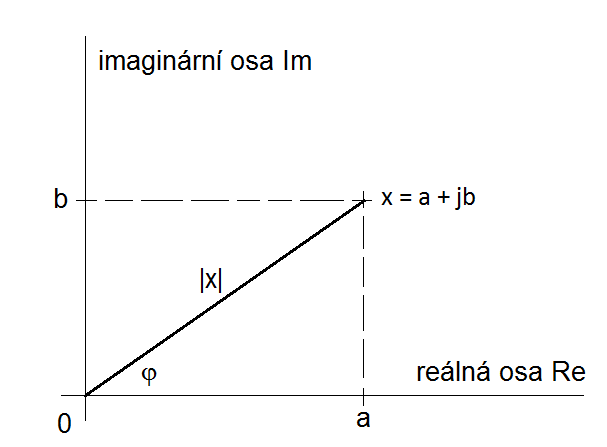
V duchu výše uvedené poznámky si můžeme komplexní číslo geometricky znázornit v tzv. Gaussově komplexní rovině, jak je na obr. Komplexní čísla 1.

Obr. 1. Znázornění komplexního čísla v Gaussově rovině.

Definice 1.6. Goniometrickým (trigonometrickým) tvarem komplexního čísla rozumíme zápis

(2)

kde reálné číslo

(3)

nazýváme modulem (absolutní nebo prostou hodnotou) komplexního čísla a úhel nazýváme fází (argumentem) komplexního čísla Pro fázi j platí (až na celistvé násobky ) vztahy

(4)

Hlavní hodnotou fáze komplexního čísla je taková hodnota úhlu pro nějž platí případně

Exponenciálním (polárním) tvarem komplexního čísla nazýváme zápis

(5)

Poznámka 1.7.

Modul r komplexního čísla je nezáporné reálné číslo a právě když
Z ekvivalence vztahů Komplexní čísla (2) a Komplexní čísla (5) je

(6)

což bude dokázáno později v kap.3.

Příklad 1.8. Vyjádřete v exponenciálním tvaru číslo

Řešení. S použitím vztahů Komplexní čísla (3) a Komplexní čísla (4) dostáváme

a

Exponenciální tvar zadaného komplexního čísla je proto

Příklad 1.9. Vyjádřete v exponenciálním tvaru číslo

Řešení.

Příklad 1.10. Vyjádřete ve složkovém tvaru komplexní číslo

Řešení.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity