Výpočet každé z N složek spektra posloupnosti pak představuje N-násobný součet součinu hodnoty signálu s reálnou i komplexní složkou jádra transformace, představované odpovídajícími hodnotami funkcí sin a cos. Takto definovaný výpočet je poměrně pracný a je otázkou, zda jej nelze optimalizovat.

Zrychlení výpočetního algoritmu se může dosáhnout využitím dříve vypočítaných mezivýsledků, resp. vynecháním zbytečných výpočtů – např. násobení nulou. Relativně zdlouhavé a opakované výpočty hodnot obou goniometrických funkcí lze usnadnit používáním předem spočítaných tabulkových hodnot pro jednu čtvrtinu periody jedné z obou funkcí. Dalšího zefektivnění výpočtu lze dosáhnout vhodným uspořádáním výpočetního algoritmu, např. tzv. rychlou Fourierovou transformací.

Abychom dokázali posoudit pracnost jednotlivých variant výpočtu diskrétního spektra diskrétního signálu je potřeba určit základní elementy výpočtu. Z definičního vztahu Časové řady II (21) vyplývá, že takové elementy jsou dva - násobení komplexního čísla a sečítání dvou čísel. Jednotku pracnosti P tedy definujme pomocí jednoho komplexního násobení a sečtení dvou čísel. Výpočet jedné hodnoty spektra signálu o vzorcích pomocí definičního vztahu představuje elementů pracnosti výpočtu, tedy Pracnost výpočtu celého spektra zahrnujícího hodnot poté představuje hodnotu Tuto hodnotu můžeme považovat za referenční pro srovnání s pracnostmi jiných variant výpočtu.

Algoritmus rychlé Fourierovy transformace má dvě z hlediska pracnosti v podstatě ekvivalentní varianty:

rozklad v časové oblasti;
rozklad ve frekvenční oblasti,

z nichž se podrobněji zabývejme principem první varianty, který je pak snadno aplikovatelný i pro postup druhý.

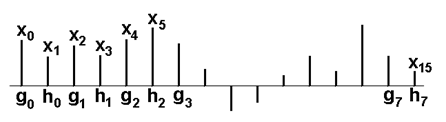
Předpokládejme, že vstupní signálová posloupnost má sudý počet vzorků. Rozdělíme ji na dvě dílčí posloupnosti (obr. Časové řady II 5):

- sudé prvky původní posloupnosti;
- liché prvky původní posloupnosti,

Obr. 5. Rozdělení signálové posloupnosti

Dále předpokládáme, že všechny posloupností (původní i obě dílčí), mají svou DFT, které jsou definovány vztahy

(22)

(23)

pro

-tou hodnotu spektra počítanou podle původního transformačního algoritmu nyní vyjádřeme pomocí dílčích výpočtů a V tom případě platí

		(24)

Když hodnoty pomocných dílčích posloupností budeme počítat podle základního definičního vztahu, bude celková pracnost součtem pracností výpočtu spekter obou posloupností a jejich spojení

(25)

tzn. dosáhneme uspoření pracnosti téměř na polovinu, pokud bude druhý člen vyjadřující pracnost zkombinování obou posloupností malý ve srovnání se členem prvním (to bude platit především pro velké hodnoty ).

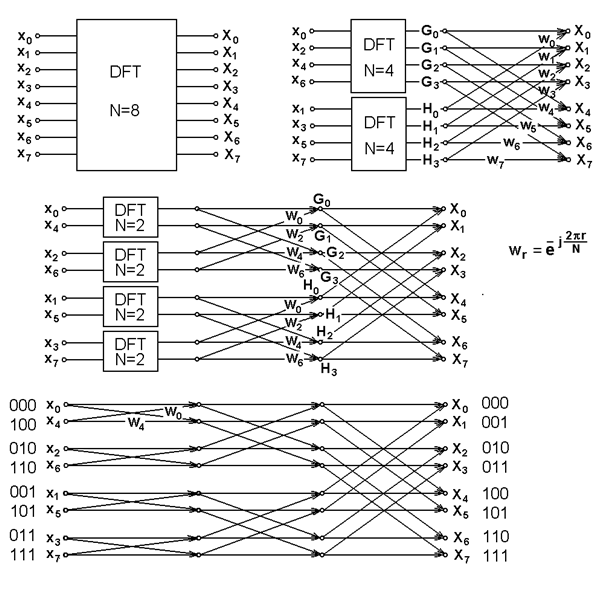
Je-li opět sudé, může se v dělení dále pokračovat – celkově je výhodné, je-li mocninou dvou, tj. platí - v tom případě lze pokračovat v dělení až ke vstupní posloupnosti (obr. Časové řady II 6).

Každý uzel ve výpočetním schématu představuje součet příspěvků reprezentovaných vstupními orientovanými hranami, přičemž jeden z obou vstupů je násoben vahou Pracnost výpočtu v každém uzlu schématu bude právě a počet uzlů v každé výpočetní vrstvě je pracnost výpočtu v celé vrstvě je Počet vrstev ve výpočetním schématu bude v případě roven a proto celková pracnost je Po velká tento výraz roste již téměř lineárně a jeho hodnoty jsou proto výrazně menší než původní pracnost s kvadratickou závislostí.

Vzhledem k postupnému dělení a uspořádávání dílčích vstupních posloupností není po dokončení rozkladu vstupní signálová posloupnost uspořádána vzestupně podle jejích indexů, nýbrž jinak. Vyjádříme-li hodnoty indexů jednotlivých vzorků binárně a tato binární čísla čteme zprava doleva (obr. Časové řady II 6), tvoří hodnoty indexů přirozeně rostoucí posloupnost - proto nazýváme uspořádání vzorků vstupní posloupnosti bitově inverzní.

Další skutečností usnadňující výpočet je existence standardních opakujících se motýlkovitých výpočetních struktur o čtyřech uzlech a čtyřech hranách, což znamená, že výpočet v rámci každé takové dílčí struktury se řídí stále stejným algoritmem. Navíc pro výpočet výstupních hodnot v každé vrstvě jsou potřeba pouze vstupní vzorky každé vrstvy, výpočet tedy může probíhat vždy jen v jedné vrstvě a lze tak šetřit výpočetní paměť.

Obr. 6. Výpočetní schéma algoritmu FFT rozkladem v časové oblasti

Příklad 4.1. Určete jak se použitím algoritmu FFT zrychlí oproti základnímu definičnímu algoritmu DFT výpočet při vzorcích, při vzorcích a při vzorcích.

Řešení. Jak bylo výše uvedeno pracnost výpočtu DFT podle definičního vztahu je podle algoritmu FFT kde je jednotka pracnosti a počet vzorků. Protože nám jde o relativní zrychlení výpočtu, dostaneme požadovanou informaci z podílu obou pracností, tj.

Pro dostáváme

pro je

a konečně pro

Pro 256 vzorků zrychlí algoritmus FFT výpočet frekvenčního spektra 32 krát, pro 1024 vzorků přibližně 100 krát a pro 1 048 576 vzorků více než 5.10⁴ krát.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity