1.1.1 Harmonická funkce
Jednou ze základních forem periodických funkcí je funkce harmonická. Vyjadřujeme ji pomocí goniometrické funkce nebo
1.Vzhledem k dalším souvislostem je užitečné zvolit jednu z obou variant jako referenční. Z některých dost dobrých objektivních důvodů, se kterými se seznámíme později, se budeme řídit následující definicí.
Definice 1.4. Harmonická funkce je určena vztahem
|
|
(3) |
kde je kladná reálná konstanta, kterou nazýváme amplitudou2 harmonické funkce (udáváme ji v jednotkách veličiny, kterou harmonická funkce popisuje),
je rovněž kladná reálná konstanta, kterou nazýváme úhlovým (kruhovým) kmitočtem (frekvencí3, rychlostí) (vyjadřujeme jej v rad/s) a
je reálná konstanta, která určuje posunutí průběhu harmonické funkce vůči počátku, tj. pro okamžik
Nazýváme ji počáteční fáze a uvádíme ji v úhlových mírách – v radiánech, resp. v úhlových stupních. Celý argument funkce kosinus určuje hodnotu okamžité fáze harmonického funkce.
 |
|
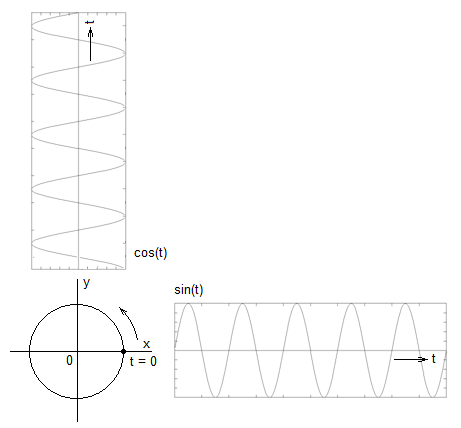
Obr. 2. Časový rozvoj průmětu kruhového pohybu bodu do os souřadnicového systému
|
Poznámka 1.5. Nejen dokonalí znalci základů goniometrie určitě ví, že argumentem goniometrických funkcí sinus i kosinus, je úhel. Tato myšlenka je podporována i skutečností, že počáteční fázi jedna ze dvou aditivních složek, z nichž se argument funkce kosinus podle vztahu Modely veličin spojitých v čase I (3) skládá, vyjadřujeme v úhlových mírách. Na druhé straně vztah Modely veličin spojitých v čase I (3) definuje harmonickou funkci jako funkci času a na to konto se čas
se také v argumentu vyskytuje. Aby měly oba součtové členy v argumentu funkce kosinus ve vztahu Modely veličin spojitých v čase I (3) úhlový rozměr, má parametr
rozměr rad/s. Součinem
se čas rozměrově eliminuje. Rozměr parametru w má úzký vztah s jeho označením úhlová rychlost, tedy úhel, který nějaký kruhový pohyb absolvuje za jednotku času.
Zbývá poslední otázka. Jak ten kruhový pohyb souvisí s funkcí kosinus? Odpověď částečně vyplývá z tzv. Eulerových vztahů Modely veličin spojitých v čase I (12), částečně i názorně z průmětů pohybu bodu umístěného na obvodu kruhu se středem v počátku souřadnicové soustavy při jeho otáčení do obou pravoúhlých souřadnicových os, jak je zobrazeno na obr. Modely veličin spojitých v čase I 2. Poloměr kruhu určuje amplitudu harmonického pohybu, frekvence kmitů je určena úhlovou rychlostí pohybu bodu. Funkce kosinus je dána časovým rozvojem průmětu pohybu do osy funkce sinus do osy
Matematická analýza jako disciplina se tímto problémem fyzikálních rozměrů logicky až tolik nezabývá. Určitě je čtenáři znám zápis ve tvaru a rozměr veličiny
se nerozebírá. Máme-li ale na mysli analýzu dat měnících se v čase, nezbývá, než tuto formalitu alespoň zmínit. Konec konců, i s ohledem na hned následující definici kmitočtu harmonické funkce.
Uvedený rozbor lze matematicky formalizovat, pokud si vyjádříme hodnotu počáteční fáze součinem V tom případě můžeme psát
|
|
(4) |
kde zůstává úhlovým kmitočtem, tj. pro daný případ konstantním parametrem a
vyjadřuje posun harmonického průběhu, tentokrát už v čase.
Základní perioda harmonické funkce je dána vztahem (je-li v radiánech)
|
|
(5) |
Se základní periodou základním úhlovým kmitočtem souvisí kmitočet harmonické funkce
pro který je
|
|
(6) |
a který v jednotkách SI udáváme v [Hz] s fyzikálním rozměrem [s-1]. Na druhé straně nikomu nic nebrání používat jiné jednotky, které lépe vyjadřují časové poměry sledovaného děje.
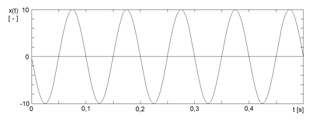
Příklad 1.6. Určete parametry harmonické funkce definované vztahem Modely veličin spojitých v čase I (7) a jejíž průběh je zobrazený na obr. Modely veličin spojitých v čase I 3
|
|
(7) |
Řešení. Amplituda je v tomto případě rovna
(je určena maximální výchylkou harmonického průběhu a jednotka, ve které její hodnotu vyjadřujeme, je dána jednotkou, ve které vyjadřujeme veličinu
), úhlový kmitočet je 2.10.
[rad.s-1], kmitočet 10 Hz a počáteční fáze
[rad].
Jak plyne z definičního vztahu Modely veličin spojitých v čase I (3), průběh harmonické funkce je pro všechny hodnoty času jednoznačně určen hodnotami tří parametrů - amplitudy úhlového kmitočtu w a počáteční fáze
Mohli bychom tedy její vlastnosti vyjádřit, kromě časového průběhu i graficky vzájemnou závislostí těchto parametrů, zpravidla vyjádřenou pomocí dvou závislostí – jednak závislostí amplitudy na úhlovém kmitočtu (resp. pouze kmitočtu), jednak v rovině počáteční fáze vs. úhlový kmitočet (resp. kmitočet). Uvidíme dále, že tento koncept zobrazení vlastností (harmonické) funkce v závislosti na jejím kmitočtu využijeme pro znázornění frekvenčního spektra4 funkce (veličiny, signálu). Pro funkci definovanou vztahem Modely veličin spojitých v čase I (7) a zobrazenou na obr. Modely veličin spojitých v čase I 3 je spektrum vyobrazeno na obr. Modely veličin spojitých v čase I 4.
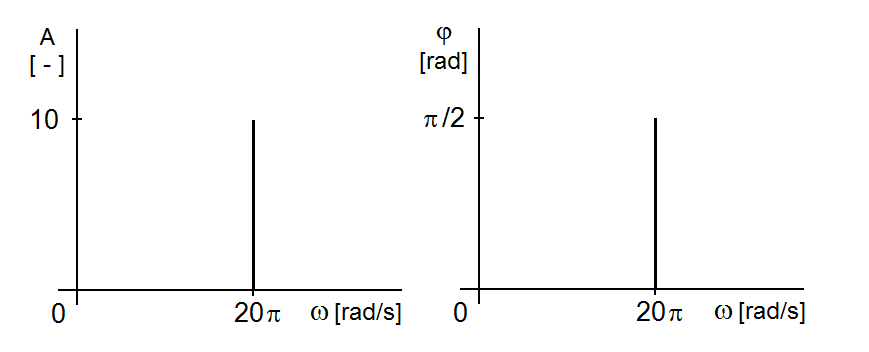 |
|
Obr. 4. Grafické vyjádření závislosti (a) amplitudy a (b) počáteční fáze na úhlové frekvenci harmonické funkce podle vztahu Modely veličin spojitých v čase I (7)
|
V dalším textu budeme spektrem rozumět závislost parametrů harmonických složek podle následující definice.
Definice 1.7. Frekvenční spektrum funkce (veličiny, signálu) je vyjádření rozložení amplitud a počátečních fází jednotlivých harmonických složek, ze kterých se funkce skládá, v závislosti na frekvenci. Závislost amplitud jednotlivých harmonických složek na frekvenci nazýváme amplitudovým spektrem, závislost počátečních fází na frekvenci fázovým spektrem.
Kromě definičního vztahu harmonické funkce podle Modely veličin spojitých v čase I (3) ji lze popsat ještě i jinými způsoby.
Blízkým způsobem definičního popisu harmonické funkce je její trigonometrický tvar. Je založen na součtovém vzorci
|
|
(8) |
Podle tohoto vztahu můžeme rozepsat definiční formuli Modely veličin spojitých v čase I (3) tak, že
|
|
(9) |
kde a
Z toho pak podělením je
a tedy
|
|
(10) |
Dále po umocnění a součtu obou vztahů máme
a po následném odmocněnní dostáváme výraz pro amplitudu
|
|
(11) |
Způsobem, jak se dostat k dalšímu tvaru harmonické funkce je aplikace tzv. Eulerových5 vztahů, které využívají pro vyjádření harmonického průběhu komplexního kalkulu6 (Komplexní čísla):
|
|
(12) |
Tohoto přístupu se obvykle využívá vzhledem k snadnějším výpočtům (za některých určitých okolností) s komplexní exponenciální funkcí než s tradičními goniometrickými funkcemi
a
Vynásobíme-li první rovnici dvěma a druhou rovnici pak po sečtení výsledků dostáváme výraz
|
|
(13) |
Znamená to, že průběh harmonické funkce definované vztahem Modely veličin spojitých v čase I (3) lze vyjádřit též jako reálnou složku průběhu komplexní funkce a harmonická funkce jako funkce času tedy je
|
|
(14) |
což odpovídá průmětu kruhového pohybu reprezentovaného pohybem vrcholu vektoru v komplexní rovině na reálnou osu.
Protože funkce cos je sudá, pak platí i
|
|
(15) |
kde je komplexně sdružená hodnota k
7. Tímto vztahem je zaveden záporný úhlový kmitočet, který lze geometricky interpretovat (fyzikální interpretace se hledá těžko) pomocí úhlové rychlosti otáčení vektoru
v opačném směru (ve směru hodinových ručiček) než v případě vektoru
Ze vztahu Modely veličin spojitých v čase I (12) pro máme
|
|
(16) |
Označíme-li
|
|
(17) |
je
|
|
(18) |
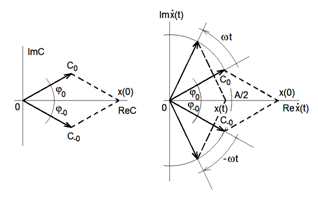
To znamená, že harmonickou funkci lze vyjádřit součtem dvou komplexně sdružených výrazů, které jsou rovny okamžitým hodnotám komplexních exponenciálních funkcí vyjadřujících navzájem protiběžné otáčení vektorů a
v komplexní rovině (obr. Modely veličin spojitých v čase I 5). Harmonická funkce je tedy opět vyjádřena pomocí komplexních exponenciálních funkcí, tentokrát sice součtem komplexně sdružených hodnot, zato bez nutnosti mnohdy nešikovně hledat reálnou hodnotu funkce
Je dobré si uvědomit, že moduly komplexních vektorů (resp. vektorů v komplexní rovině)
a
jsou dány amplitudou harmonické funkce a jejich fáze reprezentují počáteční fázi harmonické funkce.
 |
|
|
a)
|
b)
|
Na základě výše uvedených úvah lze frekvenční závislost amplitudy a počáteční fáze harmonické funkce podle vztahu Modely veličin spojitých v čase I (3) vyjádřit graficky nejen formou podle obr. Modely veličin spojitých v čase I 4, nýbrž i tak, jak je zobrazeno na obr. Modely veličin spojitých v čase I 6.
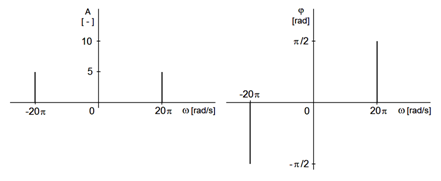 |
| Obr. 6. Grafické vyjádření závislosti (a) amplitudy a (b) počáteční fáze na úhlové frekvenci harmonické funkce definované vztahem Modely veličin spojitých v čase I (7) vyjádřené podle vztahu Modely veličin spojitých v čase I (16), resp. Modely veličin spojitých v čase I (17). |
Poznámka 1.8. Určitě stojí za povšimnutí, že amplitudové spektrum je sudé (platí ), fázové spektrum naopak liché (platí
). A tak to platí obecně.
Proč tomu tak je? Asi to souvisí s definicemi obou funkcí :). Funkce je určena odmocninou,
funkcí
1 Název funkce sinus procházel s vývojem astronomie a matematiky dle teritoria zájmu (Arábie, Indie, ..) až k arabskému džaib, což znamenalo ňadra, výstřih, vypuklost, atd. Tento význam pak ve 12. století v podstatě převzala latina, kde slovo sinus značí záhyb, oblouk, ohyb, zákrut, ale i splav, případně dutina.
2 amplituda (lat.amplitudo) – rozsáhlost, rozpětí, velikost, znamenitost, důstojnost.
3 frekvence (lat. frequentia) – hojný počet, četný dav, velká účast, zástup, hojnost, množství, četnost; ve fyzice se toto slovo začalo používat pro označení četnosti výskytu (počet výskytů určitého jevu za časovou jednotku) od 1. pol. 19. stol.
4 spektrum (lat. spectrum) – obraz, objevení, zjevení (se), vzhled; poprvé použito pro výsledek optického rozkladu světla kolem r.1670.
5 Leonhard Paul Euler (*1707 Basilej, Švýcarsko; +1783 Petrohrad, Rusko) švýcarský matematik a fyzik, který je považován za nejlepšího matematika 18. století a za jednoho z nejlepších matematiků vůbec. Významně přispěl k řešení otázek diferenciálního počtu, přispěl k základům teorie grafů, mechaniky, optiky, astronomie. Je po něm pojmenován asteroid, byl zobrazen na švýcarských bankovkách, 24. května je dokonce připomínán v luteránském kalendáři svatých.
6 V matematických textech je zvykem pro vyjádření imaginární jednotky používat písmeno i. Teorie signálů a systémů, z kterých tento text vychází, je však dominantně považována za elektrotechnickou disciplínu, kde se téhož symbolu (i) používá k označení jedné ze základních elektrotechnických veličin a to okamžité hodnoty elektrického proudu. Proto se v publikacích zabývajících se problematikou zpracování signálů používá k označení komplexní jednotky symbolu j. Budeme se držet této symboliky navzdory skutečnosti, že tyto texty jsou určeny především pro čtenáře s matematickým vzděláním a doufáme, že tato maličkost jim nezpůsobí závažné trauma.
7 Tam, kde to bude nezbytné kvůli srozumitelnosti a odlišení od proměnných nabývajících reálných hodnot, budeme označovat komplexní proměnné tečkou nad symbolem proměnné.