Pokud pomineme takové legrační operace, jako jsou součet a součin, či jiné elementární binární, např. logické operace s binárními funkcemi, je základní operací, pracující se dvěma funkcemi, používanou v teorii signálů a soustav konvoluce¹. V této kapitole se seznámíme s její definicí a některými jejími vlastnostmi, její bezprostřední praktický význam pro systémovou teorii vyplyne až z kapitol zabývajících se popisem lineárních systémů.

Definice 1.1. Konvoluce je matematická operace mezi dvěma funkcemi a téhož argumentu definovaný v případě spojitých funkcí integrálem

(1)

kde funkce se často nazývá konvoluční jádro.

Funkci jež je výsledkem konvoluce, lze považovat za nejádrovou funkci vstupující do konvolučního vztahu (zpravidla ) modifikovanou vlastnostmi konvolučního jádra (). Jak vyplývá hned z dále uvedeného komutativního zákona, význam obou vstupních funkcí lze bez jakýchkoliv následků zaměnit.

Význam konvoluce lze vnímat ještě i jinak – jako váhovaný průměr funkce v čase přičemž váhování je dáno funkcí posunutou o čas Přestože v kontextu těchto učebních textů vnímáme proměnou jako čas, může být tato proměnná obecně jakéhokoliv charakteru.

Konvolučního vztahu se používá nejen v oblasti zpracování signálů (funkcí), či jak posléze nahlédneme časových řad, nýbrž i v teorii pravděpodobnosti, statistice, počítačovém vidění a jiných technických oborech.

Pro konvoluci platí následující zákony:

komutativní zákon

(2)

Důkaz.

(3)

distributivní zákon

(4)

asociativní zákon

(5)

zákon o posunu v čase

Je-li pak

(6)

Geometrický význam konvoluce

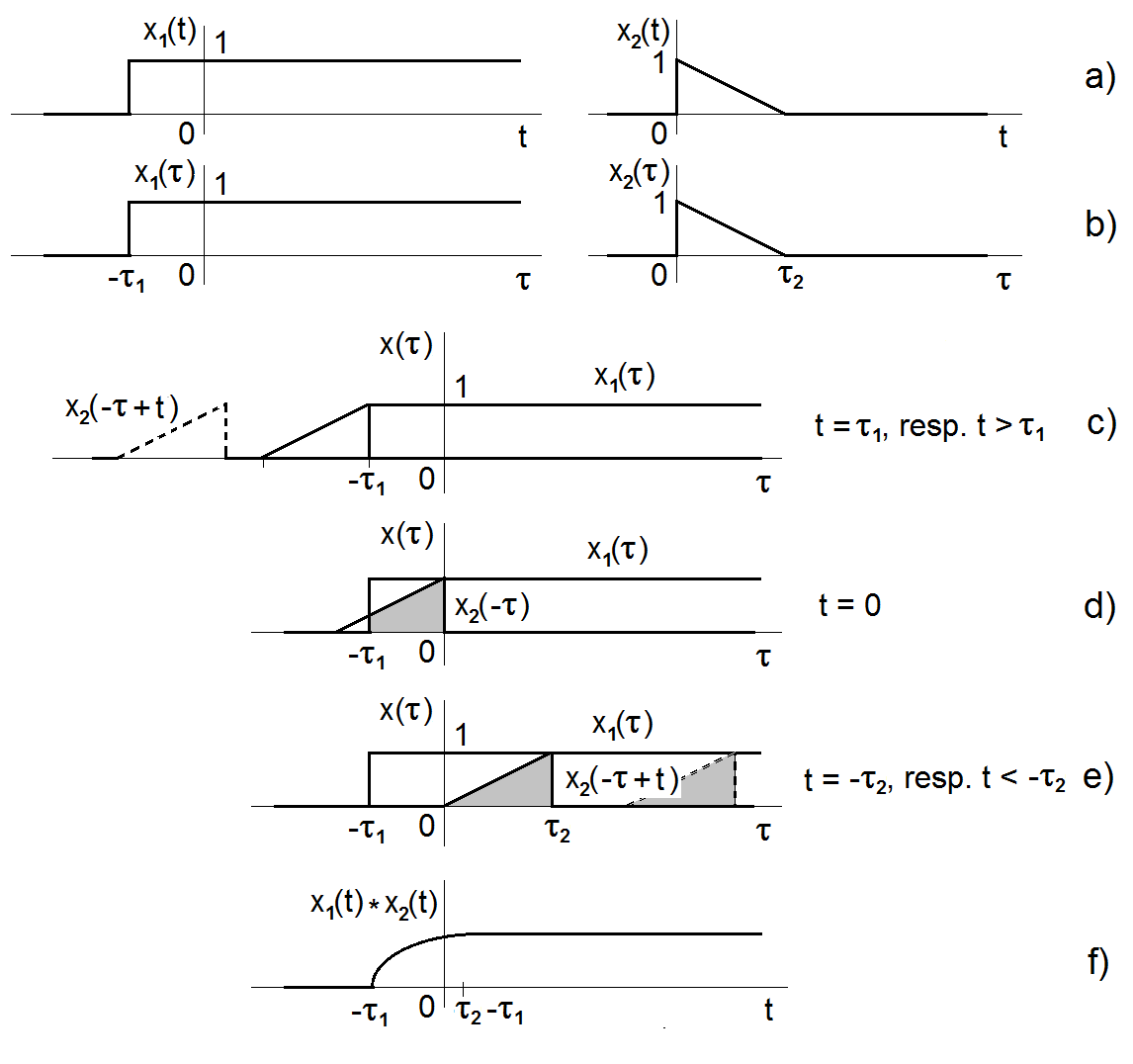
Jak vyplývá z definičního vztahu, je konvoluce rovna hodnotě určitého integrálu ze součinu dvou funkcí, z nichž jedna setrvává ve své pozici a druhá (konvoluční jádro) je invertována vzhledem ke svému argumentu (času) a posouvána o hodnotu, která odpovídá argumentu funkcí, pro který je výpočet prováděn (obr. Modely veličin spojitých v čase II 1).

Obr. 1. Geometrický význam konvoluce

Při výpočtu je potřeba si uvědomit, že integrační proměnná v definičním konvolučním vztahu je proměnná je pouze parametrem. V příkladu na obr. Modely veličin spojitých v čase II 1 jsou tři charakterem odlišné úseky:

a) kdy je součin funkce a posunuté funkce nulový (),
b) konstantní (),
c) proměnný ().

Proměnná část se v tomto případě řídí kvadratickou závislostí, jak si čtenář jistě snadno vypočítá integrací součinu lineární funkce s konstantou.

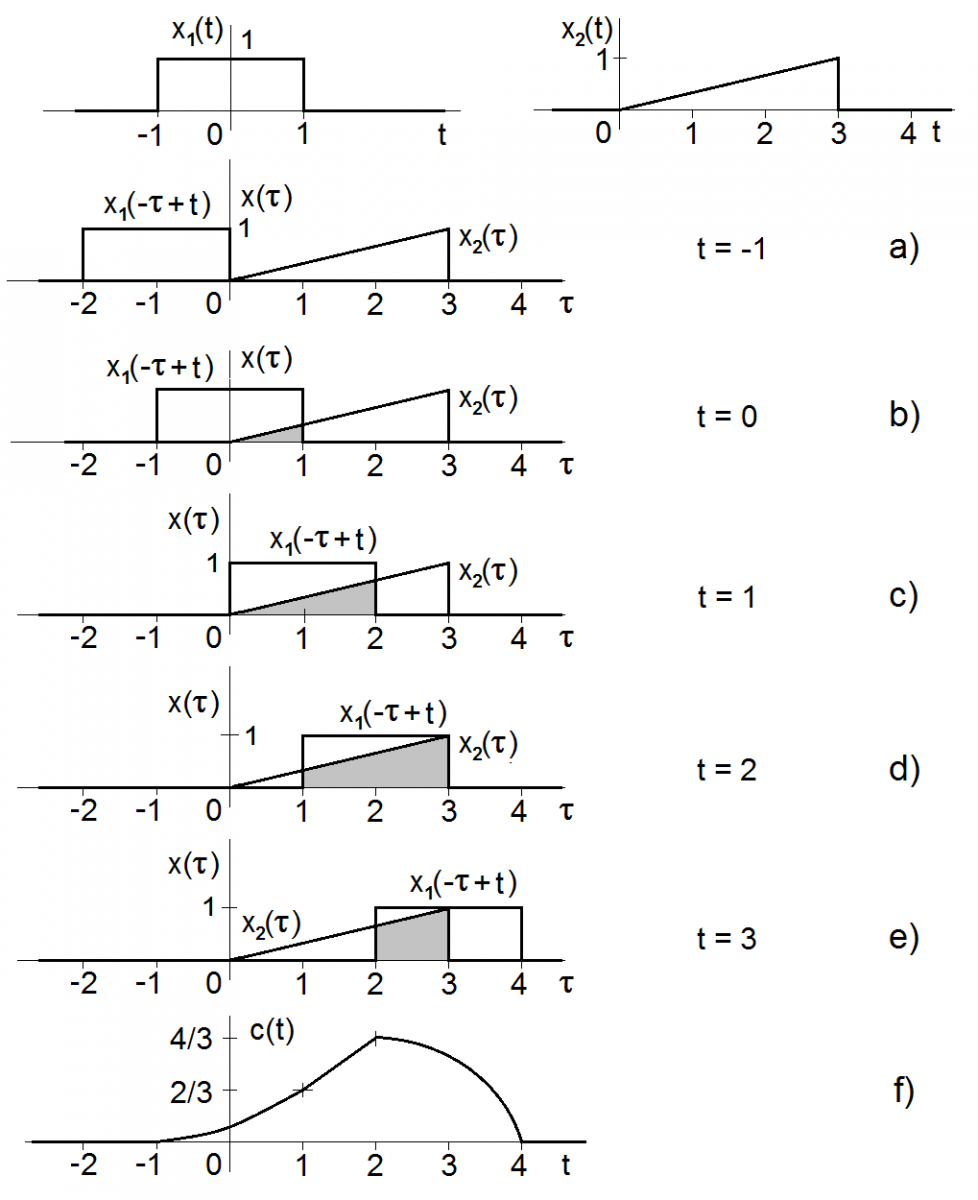
Příklad 1.2. Určete konvoluci funkcí a podle obr. Modely veličin spojitých v čase II 2.

Obr. 2. Konvoluce zadaných funkcí

Řešení. Pro řešení tohoto zadání použijme druhé varianty definičního konvolučního vztahu, tj. výrazu

V tom případě se výpočet konvoluce rozdělí podle vzájemné polohy obou funkcí na následujících pět případů podle hodnot parametru

– součin obou funkcí je v tomto případě nulový, tedy i plocha vymezená tímto součinem a konvoluce je rovna nule (obr. Modely veličin spojitých v čase II 2a);

– plocha součinu je vymezena průběhem funkce v intervalu od a polohou horní, tj. sestupné hrany funkce určené hodnotou (obr. Modely veličin spojitých v čase II 2b,c); hodnota konvolučního integrálu je

(7)

– v tomto intervalu je plocha součinu ohraničená opět funkcí tentokrát a v daném konkrétním případu v intervalu od do (obr. Modely veličin spojitých v čase II 2c,d)

(8)

– plocha součinu je nenulová v intervalu od vzestupné hrany funkce která je na pozici do sestupné hrany funkce tj. (obr. Modely veličin spojitých v čase II 2e), tedy platí

(9)

– součin obou funkcí je opět nulový, proto i konvoluční integrál. Výsledný průběh konvoluce obou funkcí daný výše vypočítanými dílčími průběhy je uveden na obr. Modely veličin spojitých v čase II 2f.

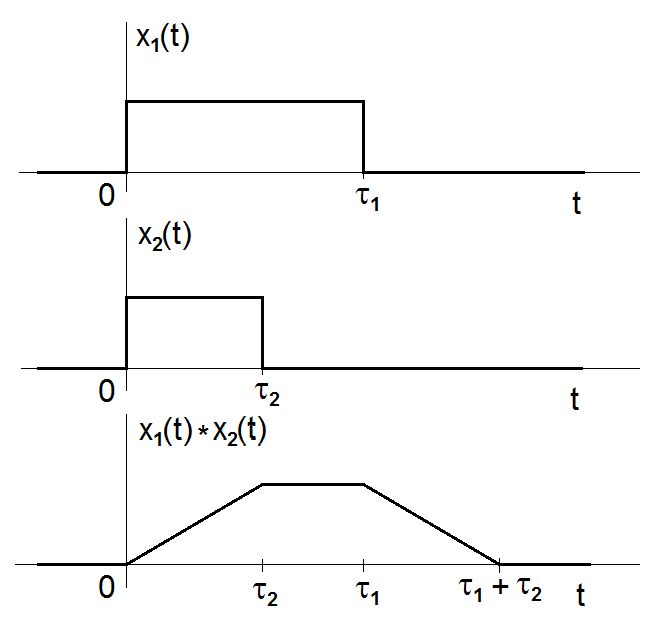
Šířková vlastnost konvoluce

Pokud jsou doby trvání (šířky, tj. doby, kdy jsou hodnoty funkcí různé od nuly) funkcí a konečné, např. v případě funkce a pro je doba trvání konvoluce obou funkcí rovna (obr. Modely veličin spojitých v čase II 3).

Obr. 3. Konvoluce dvou obdélníkových impulzů délky τ₁ a τ₂

Konvoluce funkce s jednotkovým impulzem

Výsledkem konvoluce funkce s jednotkovým impulzem je funkce

Důkaz. Z definice konvoluce vyplývá, že

(10)

Protože reprezentuje jednotkový impulz pro podle vzorkovací vlastnosti jednotkového impulzu je integrál ve vztahu Modely veličin spojitých v čase II (10) roven hodnotě v tj. Proto

(11)

¹ konvoluce (lat. convolutus; com – s-, volvere – valit, válet, otáčet) – stočený, sbalený, ovinutý

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity