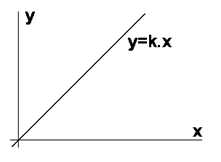
1 Linearita

Mnohé základní pojmy teorie systémů již byly zavedeny v kapitole počáteční 2.2 Systém. V tomto místě se podrobněji zabývejme linearitou systémů. Linearita je vlastnost v reálném světě ne příliš častá, na druhé straně, pokud je systém lineární, velice se jeho matematický popis zjednoduší, zjednoduší se i jeho analýza. Tyto vyjmenované důvody jsou ale jen teoretické. Má linearita i praktický význam, když je, jak je výše uvedeno, v reálném světě tak zřídkavá? Reálné objekty a nejen biologické jsou opravdu především nelineární. Na druhé straně ale zpravidla fungují pouze v omezeném rozsahu svých možností a je ke zvážení, zda je možné v tomto omezeném rozsahu chování objektu linearizovat. Pokud ano, je to skvělá příležitost pro lineární systémy.

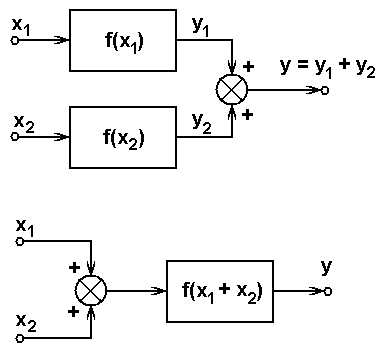
	Obr. 1. Schematické vyjádření vztahů principu superpozice

Definice 1.1. Lineární systém s převodní funkcí je takový, pro nějž platí princip superpozice, definovaný následujícími dvěma vztahy (obr. Matematický popis systémů pracujících ve spojitém čase I 1):

		(1)

kde je konstanta.

Někdy se lze setkat i s obecným vyjádřením principu superpozice ve tvaru

(2)

kde jsou konstanty. Princip superpozice můžeme obecně vyložit i tak, že je-li nějaký komplexní problém lineární, můžeme jeho řešení získat váhovaným součtem řešení jeho jednotlivých dílčích částí.

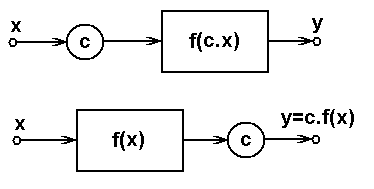
Příklad 1.2. Ověřte linearitu systémů s převodními funkcemi podle obr. Matematický popis systémů pracujících ve spojitém čase I 2.

a)	b)
Obr. 2. Příklady převodních funkcí systémů – a) lineární funkce procházející počátkem; b) lineární funkce s absolutním členem.

Řešení.

a)

kde reprezentuje výpočet dle levé strany prvního definičního vztahu principu superpozice, dle jeho pravé strany, výpočet dle levé strany druhého vztahu a výpočet dle jeho pravé strany.

Systém s převodní funkcí podle obr. Matematický popis systémů pracujících ve spojitém čase I 2a splňuje princip superpozice, je tedy lineární.

b)

Systém s převodní funkcí podle obr. Matematický popis systémů pracujících ve spojitém čase I 2b nesplňuje princip superpozice, tedy lineární není, přestože jeho převodní funkce má lineární charakter.

Co tedy vyplývá z tohoto poznání? Princip superpozice definující linearitu převodní soustavy je něco trošku jiného než pouhý lineární (tj. přímkou či rovinou definovaný) popis vzájemného vztahu mezi vstupní(mi) a výstupní(mi) veličinou(ami).

Známe některé matematické operace, které jsou lineární z hlediska principu superpozice? Určitě ano. Na příklad bude z hlediska dalšího textu užitečné si připomenout, že lineární podle principu superpozice jsou derivace i integrace. Vždyť přece ti, kteří o derivování a integrování vědí i jen to základní, určitě znají vztahy pro derivaci

a pro integraci

A to je přece přesně to jak je definován princip superpozice.