4.1 Základní pojmy

Ve zcela úvodní výukové jednoce jsme si zavedli obecnou definici stability jako schopnost systému udržet si při změně vstupů a stavů svých prvků nezměněnou vnější formu (chování) i navzdory třeba i velice bouřlivým procesům probíhajícím uvnitř systémů. O něco méně obecně lze stabilitu definovat jako vlastnost systému, která charakterizuje jeho schopnost udržet si své chování či rysy v předepsaných mezích i za případného vnějšího rušivého působení. Navzdory obecnosti těchto definic, vyplývá z nich, že stabilita je vnitřní vlastností systému. Souvisí ale s vnitřním stavem systému, který označujeme jako rovnovážný stav.

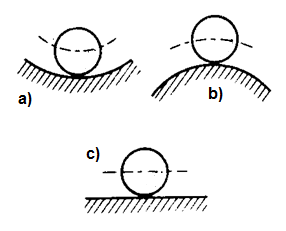
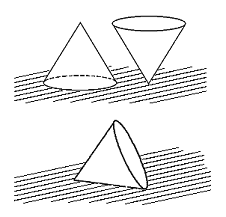
Obr. 3. Různé situace stabilních a nestabilních systémů, příp. systémů na mezi stability

Rovnováha je stav systému, vzniklý vyrovnáním vlivů na systém působících. Rovnovážné stavy mohou být stabilní, neutrální (tzv. na mezi stability) nebo nestabilní. Stabilita obecně závisí jednak na vlastnostech samotného systému (zejména v případě lineárních systémů), jednak může záviset i na charakteru a působení prostředí na systém (v případě nelineárních systémů). Stabilitu či nestabilitu rovnovážného stavu vyšetříme pomocí malého vychýlení systému z rovnovážného stavu. Pokud se systém vrátí do původního stavu, je rovnovážný stav systému stabilní. Pokud po vychýlení opustí systém původní rovnovážný stav, je rovnovážný stav nestabilní. Konečně, pokud působení malé velikosti vychýlí systém z rovnovážného stavu a systém zůstává v tom stavu, do kterého se dostal po vychýlení, hovoříme o mezní stabilitě.

Příklady těchto situací jsou zobrazeny na obr. Matematický popis systémů pracujících ve spojitém čase II 3. V levé polovině obrázku je koule na podložkách různého tvaru. Ať se koule pootočí jakýmkoliv způsobem, zůstává sama o sobě v tomtéž stavu. Chování celého systému ovlivňuje tvar podložky. Situace a) popisuje chování koule uvnitř kulové plochy většího poloměru. Ať je koule jakkoliv vychýlena, vrací se v tomto případě zpět do původního rovnovážného stavu, zpravidla tlumenými kmitavými pohyby - systém v tomto rovnovážném stavu je stabilní. Případ b) popisuje chování koule na vrcholu konkávní kulové plochy. Při vychýlení z rovnovážné pozice tuto polohu opouští a již se do ní nevrací - rovnovážný stav je v tomto případě nestabilní. Konečně na rovné podložce se koule působením vnější síly přemístí do nové polohy a v této poloze zůstává - rovnovážný stav je neutrální, resp. na mezi stability. Kužely v pravé polovině obrázku reprezentují systém, jehož rovnovážné stavy závisejí na systému samotném, nikoliv na vlastnostech prostředí, ve kterém se nachází. Stojí-li kužel na své podstavě, je ve stabilním rovnovážném stavu a ani malé vychýlení kuželu nezpůsobí jeho převrácení. Naopak, stojí-li kužel na svém vrcholu, nachází se v nestabilním rovnovážném stavu, jakékoliv sebemenší vychýlení způsobí převrácení kužele. Poslední poloha, kdy se kužel leží na svém plášti, reprezentuje neutrální rovnováhu. Kužel se působením vnější síly pootočí a zůstává v nové poloze.

Pro určení stability používáme dva základní přístupy, vyplývající ze dvou výše zmíněných systémových jevů:

• stabilita vynuceného pohybu,
• stabilita vůči počátečnímu stavu (daná konvergencí přirozené odezvy).