V různých experimentálních oborech - v medicíně např. v epidemiologii, fyziologii, v biologii, environmentalistice, ekonomii, demografii, sociologii - se často zpracovávají data, která popisují nějakou konkrétní situaci v jednom určitém čase, příp. na čase vůbec nezáleží, nebo naopak vyjadřují hodnoty určitých zajímavých veličin jak se mění v čase.

Náplní následujícího textu bude poslední zmíněná situace.

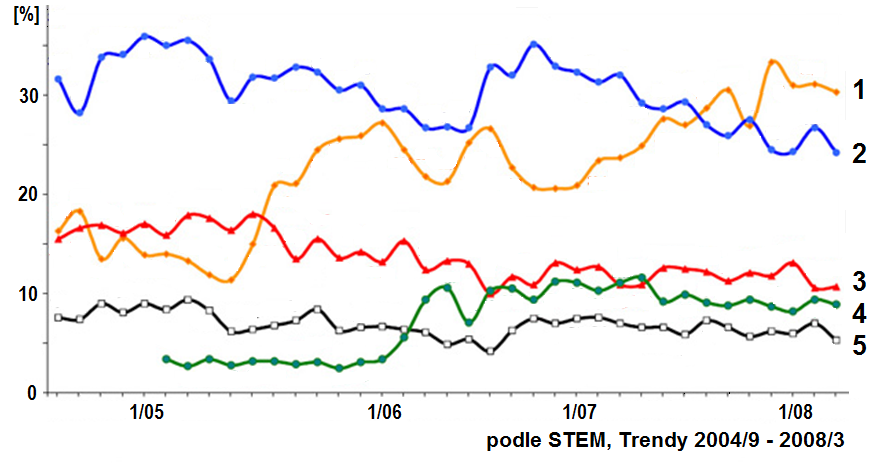
Obr. 1. Časový průběh preferencí politických stran v ČR za období září 2004 až březen 2008

Uvažme případ, který je zobrazen na obr. Kapitola počáteční 1. Křivky na něm reprezentují hodnoty aktuálních preferencí politických stran v České republice mezi roky 2004 – 2008. Křivky jsou znázorněny jako spojité čáry, nicméně vznikly interpolací mezi zjištěnými hodnotami v konkrétních časových okamžicích – zpravidla po měsíci. (Průzkumy ale většinou neprobíhaly o prázdninách, nejdelší výpadek nastal v letních měsících roku 2006, časové intervaly mezi jednotlivými hodnotami tudíž nejsou stejné. Jak dále nahlédneme v dalších lekcích, z hlediska analýzy to není zrovna nejvhodnější situace.) Je zřejmé, že preference politických stran stále nějaké jsou. Jsou definovány v jakémkoliv časovém okamžiku, jsou to veličiny v čase spojité. To, že známe jejich hodnoty jen v některých časových okamžicích, je formálně důsledkem tzv. vzorkování^1.

Frekvence průzkumů (zpravidla jednou za měsíc) je v tomto případě dána organizačními a ekonomickými kritérii a důvody. Jak je ale dále uvedeno v jedné z dalších kapitol, lze pro stanovení největšího možného intervalu mezi každými dvěma vzorky definovat teoretické pravidlo, které zajistí, že ze vzorků původně v čase spojité veličiny lze její průběh kompletně zrekonstruovat. Volba způsobu vzorkování původně spojitých veličin by měla být jednou ze základních úloh při zpracování časově proměnných spojitých veličin. Řešení této úlohy může být vázáno na různé okolnosti a požadavky. Pokud není zájem či se nelze řídit teoretickými doporučeními (jak o nich bude řeč později), je nezbytné býti si vědomi možných následků při zpracování navzorkovaných dat a počítat s nimi.


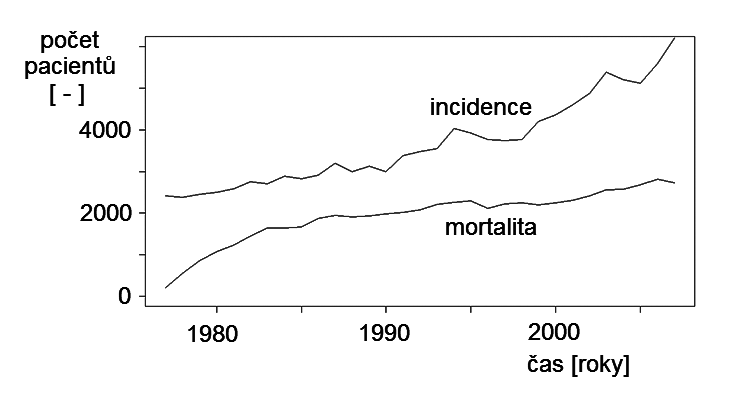
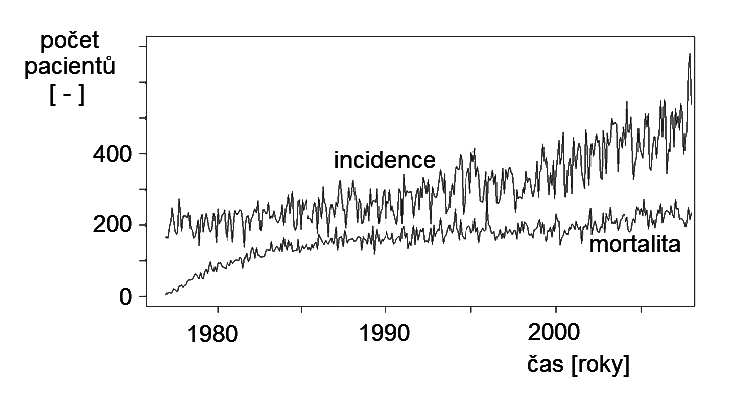
a) roční vzorkování	b) měsíční vzorkování
Obr. 2. Vývoj incidence a mortality zhoubného nádoru prsu v ČR – a) roční vzorkování; b) měsíční vzorkování

Poněkud jinou situaci lze sledovat na veličinách zobrazených na obr. Kapitola počáteční 2. Zobrazené křivky na obou grafech tohoto obrázku představují časový vývoj hodnot incidence a mortality na zhoubný nádor prsu v ČR vyjádřených absolutními počty pacientek. Na rozdíl od předchozího „politického“ příkladu, který popisoval aktuální okamžitý stav hodnot sledovaných veličin, mají tyto údaje charakter kumulační (integrální) za určité časové období. Hodnoty sledovaných veličin známe až v okamžiku ukončení intervalu, ve kterém počty nových onemocnění či úmrtí kumulujeme. Jejich hodnoty tedy nejsou definovány pro všechny časové okamžiky, ale jen pro určité zvolené časy určující charakter vzorkování. Obě zobrazované veličiny proto primárně nejsou v čase spojité, nýbrž primárně v čase diskrétní², byť jsou jednotlivé hodnoty na obrázcích proloženy spojitou čarou.

Na obr. Kapitola počáteční 2.a) jsou počty stanoveny kumulací za celý kalendářní rok. Zobrazené křivky jsou zde poměrně hladké, bez výrazných změn úrovně, v podstatě zobrazují pouze základní dlouhodobou tendenci vývoje onemocnění. Na obr. Kapitola počáteční 2.b) jsou zobrazeny tytéž veličiny s tím, že počty nových onemocnění či úmrtí jsou shromažďovány v měsíčních intervalech, tedy dvanáctkrát častěji. Je patrné, že se zcela změnil charakter dat – zůstalo vyjádření základní dynamické tendence i když s hodnotami dvanáctkrát menšími, ovšem výrazně se projevila kmitavá složka. Na tomto příkladu se ukazuje, že zvýšení frekvence vzorkování v datech odhalilo některé závislosti, které z původního vyjádření nebyly zřejmé. Frekvence vzorkování tedy může být podstatná pro zachycení jednotlivých složek sledovaného děje.

Co by mohlo být cílem zpracování takovýchto dat?

Možná nejzajímavějším výsledkem zpracování by mohla být predikce budoucího průběhu časové řady. V prvním, politickém případě by to byl odhad preferencí v období navazujícím na interval sledování (důležité pro úvahy o zachování či změně strategie prezentace politických stran), v druhém, epidemiologickém případě by to byl odhad počtu nových onemocnění, resp. s tím související vývoj mortality (hodnoty, které mohou být důležité např. pro plánování budoucí lůžkové kapacity zdravotnických zařízení nebo finančních prostředků pro léčení pacientů).
Dalším, určitě neméně zajímavým výsledkem zpracování či modelování dat by mohlo být porozumění dějům, které dávají vzniknout zjištěným průběhům. Co způsobilo výrazný nárůst oranžové křivky č.1 v druhé polovině roku 2005 na obr. Kapitola počáteční 1 a co charakterizuje, resp. čím je dáno postupné dokmitávání po nárůstu zelené křivky č.4 na začátku roku 2006? Čím jsou dány „zuby“ na křivce incidence na obr. Kapitola počáteční 2 v první polovině 90. let a kolem roku 2003? Odpovědi na tyto otázky se však jen obtížně získávají pouze na základě datové analýzy, zde je zpravidla potřeba použít i apriorní informace o vlastnostech a chování analyzovaného objektu.
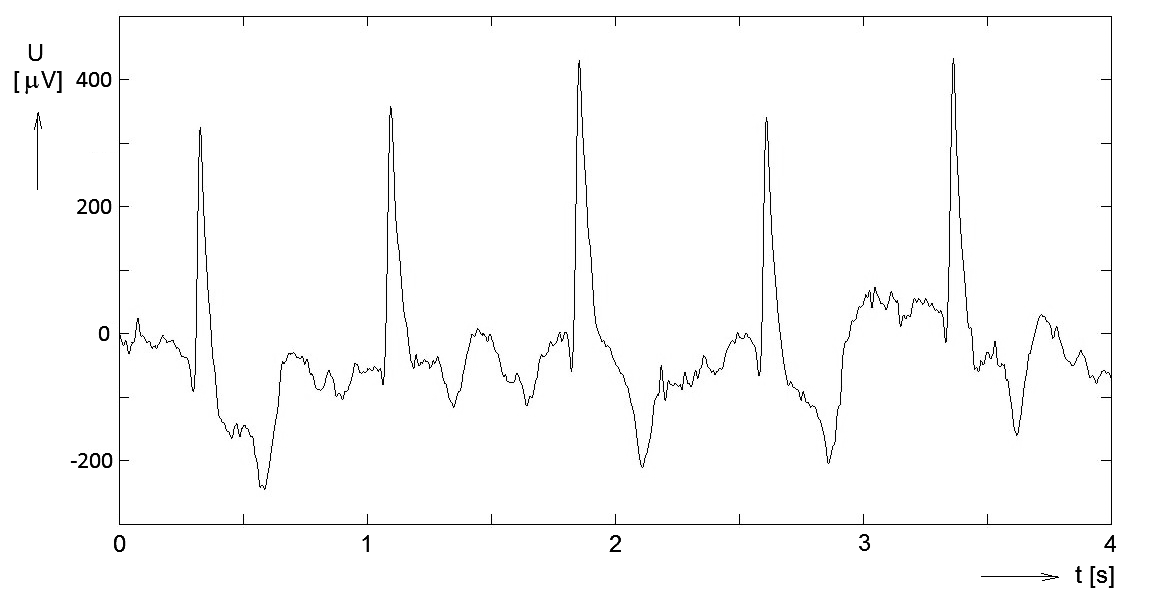
Výsledkem zpracování může být klasifikace/diagnóza stavu objektu, podle tvaru křivky generovaném daným objektem. V tomto případě je z určitého hlediska potlačena časová dynamika křivky. Zpracovávanou křivku či její podstatnou část lze považovat za vektor hodnot, který daný úsek křivky vyjadřuje bodem v tolikarozměrném prostoru, kolik vzorků má daný zpracovávaný úsek. (Viz třeba analýza stavu kardiovaskulárního systému koně na základě průběhu jednoho srdečního cyklu jeho signálu EKG – obr. Kapitola počáteční 3).

Obr. 3. Elektrokardiografický signál (EKG) koně v kroku

S předchozí diagnostickou úlohou souvisí tzv. monitorování časového vývoje sledované veličiny a detekce významných změn jejího průběhu. Toto je v podstatě také diagnostická úloha, ale s časově dynamickou složkou – je potřeba odlišit standardní stav od situace, kdy se začíná něco dít. Klasicky to může být např. úloha sledování pacientů v kritickém stavu na jednotce intenzivní péče.

Všechny tyto zmíněné úlohy jsou zpravidla založeny na matematickém popisu/modelu průběhu dat ve sledovaném období. Matematický model by měl na jedné straně být co nejjednodušší (aby se s ním dobře pracovalo), na druhé straně co nejpřesnější nebo možná co nejvýstižnější (aby co nejlépe reprezentoval sledované děje, resp. alespoň jejich nejdůležitější složku).

Aby bylo možné model dat syntetizovat, je potřeba buď vědět něco o podstatě dějů, které data generují, nebo provést analýzu dat a jejich časového vývoje, tj. pokusit se rozložit zobrazené časové průběhy na dílčí složky.

Principy tvorby modelů, které vychází z apriorní informace o procesech probíhajících ve sledovaném objektu lze najít např. v Úvod do matematického modelování. V tomto textu se budeme zabývat především druhým z uvedených postupů, tj. rozkladem časového průběhu dané veličiny na základní složky.

Základní skladba, ze které jakékoliv zpracování časového průběhu dat vychází, je dělení na složku, která deterministicky jednoznačně souvisí se zkoumaným dějem, resp. stavem analyzovaného objektu (má-li pacient chřipku, má zvýšenou tělesnou teplotu) a na složky, které s ním (deterministicky) nesouvisí. Nedeterministická složka formálně souvisí s nějakými dalšími vlivy, kterým možná rozumíme, ale jsou příliš složité, než abychom se zabývali jejich podrobným exaktním popisem nebo zatím příčinám vzniku této složky informace ani nerozumíme. Pokud data složku, z pohledu dané úlohy deterministicky související se zkoumaným procesem neobsahují, neexistuje sebemenší důvod k řešení úlohy pomocí těchto dat.

Obecným cílem jakéhokoliv zpracování dat je odhalit, analyzovat, kvantifikovat či klasifikovat právě tuto deterministickou složku.

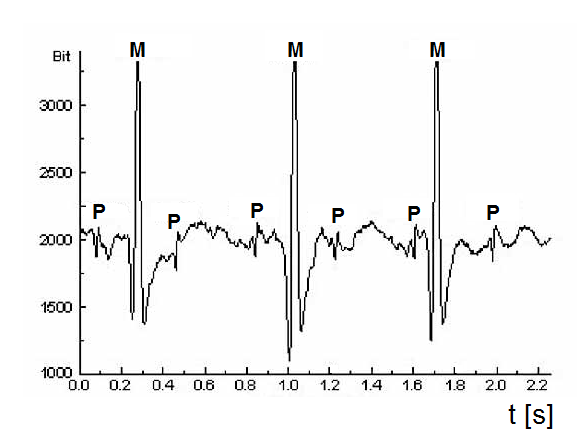
Členění na deterministickou a nedeterministickou složku (ve smyslu vazby na sledovaný stav analyzovaného objektu) je ale velice vázáno na charakter řešené úlohy. Z toho vyplývá, že k separaci nedeterministické a deterministické složky, resp. k výběru „správné“ deterministické složky je často třeba určitá nadstavbová znalost dalších souvislostí a okolností spojených s řešenou úlohou. Na obr. Kapitola počáteční 4 je znázorněn elektrokardiogram těhotné ženy, který jednak obsahuje průběh EKG matky, jednak EKG plodu, navíc i další rušivé složky způsobené způsobem měření, projevy prostředí, atd. Chceme-li sledovat stav rodícího se dítěte, bude důležitá složka elektrické aktivity srdce plodu a EKG matky bude parazitní. Při sledování stavu matky (nutno říci, že při porodu to nebývá standardní úloha) lze za parazitní složku považovat kmity související s komorovou aktivitou srdce plodu.

Obr. 4. EKG těhotné ženy – M - záznam projevů depolarizace buněk srdečních komor matky; P - záznam projevů depolarizace buněk srdečních komor plodu

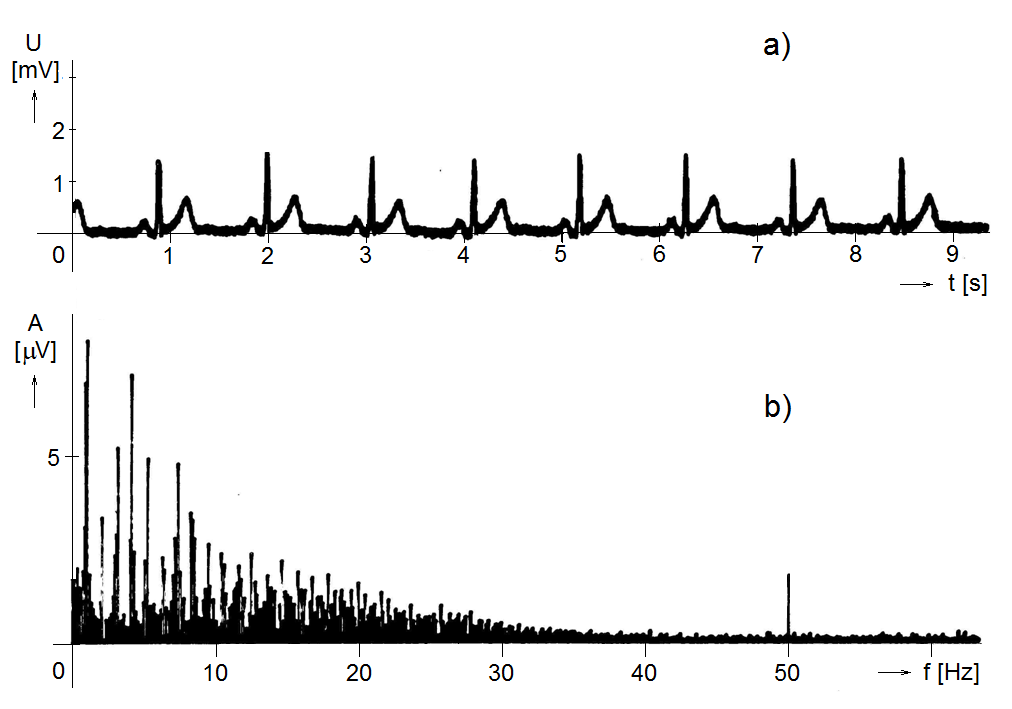
Trochu jiným příkladem žádoucí a nežádoucí složky signálu je situace na obr. Kapitola počáteční 5, kde v horní části obrázku je časový průběh jednoho svodu záznamu signálu EKG, zarušeného naindukovaným síťovým napětím. To, že širší stopa křivky EKG je způsobená síťovým kmitočtem je zcela jasně patrno z frekvenčního spektra (pojem bude podrobně objasněn v následujících kapitolách) v dolní části obrázku, kde je zřetelně vidět čára, jejíž velikost vyjadřuje míru přítomnosti harmonického průběhu o frekvenci 50 Hz.

Obr. 5. Časový průběh (a) a frekvenční spektrum (b) signálu EKG ovlivněného síťovým rušením. Rušení se v časové závislosti projevuje rozšířením stopy záznamu, ve frekvenčním spektru výraznou čarou na frekvenci 50 Hz.

Jiným přístupem, založeným na víceméně obecných vlastnostech časových řad, je dělení průběhu na:

trend³ vyjadřující monotónní dlouhodobé tendence sledovaných křivek – např. v obr. Kapitola počáteční 1 kontinuálně klesající trend preferencí u křivky 3 od poloviny roku 2005, rostoucí preference u jinak velice neuspořádaného průběhu křivky 1; zjevně kontinuálně stoupající tendence incidence i mortality, způsobené nádorovým onemocněním prsu na obr. Kapitola počáteční 2.a), konec konců i na obr. Kapitola počáteční 2.b).
oscilační⁴ charakter –
- dlouhodobé oscilační děje s periodou významně delší než je doba sledování dané veličiny; občas bývá slučována s trendovou složkou a toto spojení se nazývá drift⁵.
- segmenty s relativně vyšší frekvencí kmitů (v analyzovaném úseku se vyskytuje několik cyklů průběhu) - často tuto kmitavou složku označujeme jako sezónní (na obr. Kapitola počáteční 1 většina křivek kmitá s poměrně vysokou frekvencí, u křivky 2 i pomalejší oscilace s periodou přibližně dva roky; zajímavý průběh má křivka 4, která z nízké úrovně po začátku roku 2006, zřejmě působením nějakého vnějšího vlivu rychle a výrazně vzrostla - charakteristický je u této křivky i výskyt tlumených oscilací po tomto rychlém nárůstu u jinak relativně kmitů prosté časové závislosti. Na obr. Kapitola počáteční 2 se kmitavá sezónní složka objevila až při zvýšení frekvence vzorkování (obr. Kapitola počáteční 2.b)), přičemž popisovala opravdu sezónní časový vývoj onemocnění, resp. úmrtnosti během roku.
nedeterministická šumová složka –je zpravidla ovlivněná různými vlivy buď přímo u zdroje (zvýšená tělesná teplota je u někoho nižší, u někoho vyšší – je důležité vědět proč nebo není třeba se tím zabývat?), nebo způsobená chybami při měření či přenosu dat (chybná metoda měření, konečná přesnost měřicího zařízení, zdravotní sestra se spletla, když zapisovala teplotu do chorobopisu, …). Konečně může být dána i použitím chybného či nepřiměřeného předzpracování dat. Pro vyjádření nedeterministické složky dat lze použít různé matematické prostředky, nelze ale rovnou a priori tvrdit, že je tato složka náhodná, byť se tak často děje. Je užitečné si uvědomit, že náhodnost není vlastnost, která by byla vlastní analyzovaným dějům, nýbrž je to vlastnost datům vnucovaná nástrojem používaným k jejich zpracování. V tomto případě téměř dominantně užívanou teorií pravděpodobnosti, resp. statistikou. Ovšem existují i jiné způsoby popisu nejistoty v datech, např. pomocí teorie mlhavých (fuzzy) množin, resp. fuzzy algebra, která základní vyjádření nejistoty pomocí hustoty rozdělení pravděpodobnosti nahrazuje funkcí příslušnosti nebo třeba teorie hrubých množin, která hodnotu pravděpodobnosti nahrazuje tzv. faktorem důvěry. Uvedené rozdíly samozřejmě nejsou jen terminologické, reprezentují i jiné způsoby zpracování dat a interpretace získaných výsledků. Proč se ty další způsoby popisu a zpracování nejistých dat tak málo uplatňují je dáno především délkou historického vývoje zmíněných disciplín.

Výsledkem analýzy není jen nalezení jednotlivých složek, nýbrž i ocenění jejich vzájemného vztahu, daného buď apriorně (a ověřením na základě hypotetického předpokladu) či aposteriorně (jako výsledek analýzy). Dva základní modely vzájemného vztahu dílčích složek analyzovaných dat jsou aditivní (výsledný průběh je dán součtem dílčích složek) a multiplikativní (výsledný průběh je dán součinem dílčích složek). Možná je i kombinovaná, částečně aditivní, částečně multiplikativní směs jednotlivých datových složek.

Poznámka na okraj. Multiplikativní model je bezesporu komplikovanější, vede k popisu nelineárních vztahů. Z toho důvodu je mnohdy patrná snaha úlohu zjednodušit logaritmickou transformací dat, která multiplikativní vazby převádí na aditivní. Zpravidla je ale něco za něco. Logaritmováním se významně mění charakter datových hodnot, který za zjednodušení vazeb mezi jednotlivými složkami analyzovaných veličin může zaplatit fatálním zkomplikováním analýzy jednotlivých složek. Navíc jak známo nelze logaritmovat záporné hodnoty. Problém jistě snadno řešitelný, ovšem jen za cenu přidání k datům něčeho, co v nich původně nebylo.
Je proto vždy potřeba zvážit, zda zjednodušení dílčí fáze analýzy znamená také zjednodušení řešení celé úlohy. A to je rada obecná.

¹Vzorkování je postup výběru jednotlivých pozorování, na jehož základě získáváme informaci o vlastnostech sledované skutečnosti či jevu. Vzorkování v ideálním případě zachovává informaci, obsaženou ve vzorkovaném ději.

2diskrétní (franc. discret, lat. discernere, rozlišovat; discretus rozdělený) v matematice, v technice a v informatice znamená nespojitý, nebo také digitální. V technické odborné literatuře je však pojem diskrétní (v čase) považován za podmnožinu pojmu digitální (je diskrétní i co do úrovně).

³trend (angl.) – vývojová tendence, celkový obecný sklon směřování dlouhodobé dynamiky; v tomto smyslu se používá od konce 19. století.

⁴oscilace (lat. oscillatio) – houpání (se), kolébání (se), kývání (se), resp. kmitání nebo kmitavý děj, změna nějaké veličiny vykazující opakování, střídání nebo tendenci k němu; slova oscillum se používalo pro označení malé masky boha Dionýza (Baccha), která se věšela v blízkosti vinic a její houpavý pohyb způsobený vlivem větru plašil ptáky.

⁵drift (angl. od 13. stol. ve významu a being driven) – v současné době má mnohé významy podle disciplin, v nichž se používá, vesměs vyjadřující určitou formu pomalého pohybu – kontinentální drift, genetický drift, v motorismu pro označení pomalého řízeného přetáčivého smyku; zde jeho význam vnímáme ve smyslu pomalých časových změn sledované veličiny.

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity