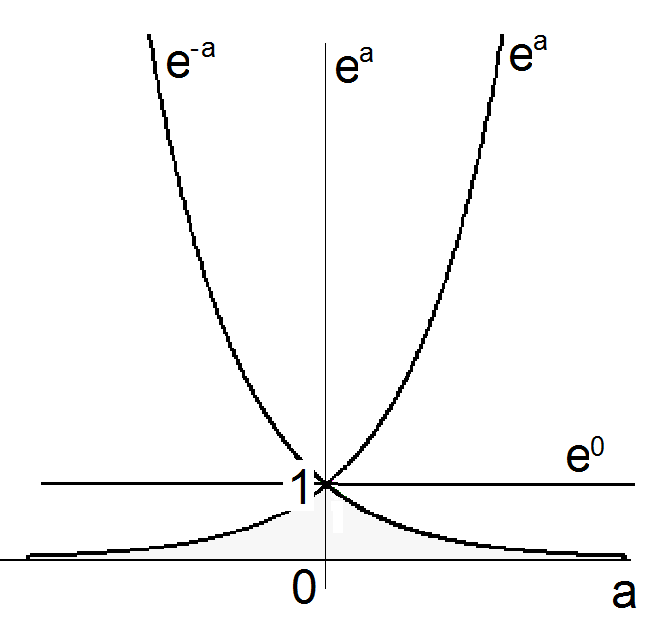
Průběh exponenciální funkce s komplexním exponentem je tedy určen součinem exponenciály s reálným exponentem a exponenciály s ryze imaginárním exponentem. Exponenciála s reálným exponentem má známý průběh, v závislosti na znaménku exponentu má typický rostoucí (pro kladný exponent) či klesající (pro záporný exponent) průběh, případně konstantní průběh pro nulový exponent (obr. Komplexní čísla 4). Abychom si učinili představu o celkovém průběhu exponenciály s obecným komplexním exponentem, musíme určit průběh exponenciály s ryze imaginárním exponentem. K tomu bude užitečné rozvinout funkce resp. do mocninné řady. Ze dvou typických způsobů rozvoje funkce do mocninné řady, pomocí Taylorova řady a Maclaurinovy řady, se zabývejme druhým, sice jednodušším a v podstatě méně, ale dostatečně obecným způsobem pro vztažný bod

Obr. 4. Průběh exponenciální funkce s reálným exponentem

Pro Maclaurinův rozvoj funkce do nekonečné řady platí

(20)

Příklad 3.1. Rozviňte do Maclaurinovy řady funkce a

Řešení. Rozvoj funkce pro

Z těchto dílčích hodnot derivací plyne, že

(21)

Je užitečné si všimnout, že funkce která je lichá, se skládá pouze z lichých mocniných členů.

Rozvoj funkce pro

Z těchto dílčích hodnot derivací pak plyne, že

(22)

Rozvoj sudé funkce obsahuje pouze sudé mocniny argumentu.

Konečně, Maclaurinův rozvoj exponenciální funkce pro je:

Z těchto dílčích hodnot derivací pak plyne, že

(23)

Příklad 3.2 Určete pomocí vypočítaných mocninných řad pro funkce a nalezněte vztah mezi funkcemi a

Řešení. Do odvozeného mocniného vztahu Komplexní čísla (23) dosadíme za tj. se symbolem jenž lépe navozuje představu úhlové veličiny. Potom s využitím vztahu Komplexní čísla (1) platí, že

(24)

Tento vztah lze rozdělit na reálnou a imaginární část tak, že je

(25)

a z toho s využitím vztahů Komplexní čísla (21) a Komplexní čísla (22) je

(26)

což je právě rovno dříve uvedenému vztahu Komplexní čísla (6).

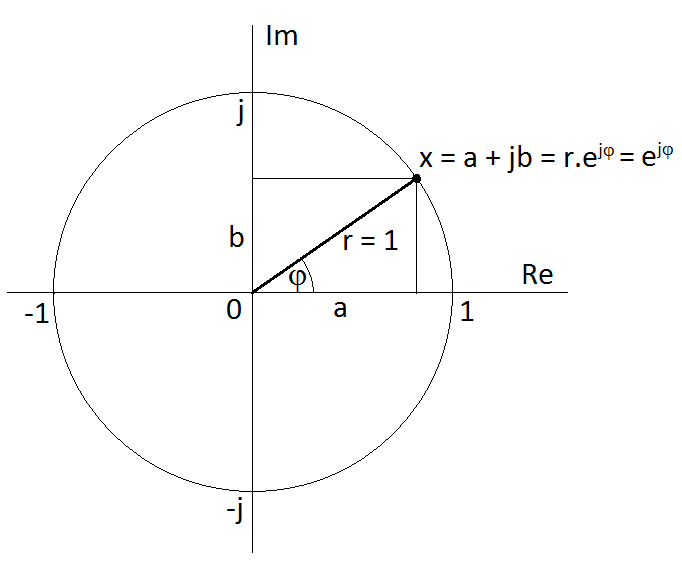
Co z odvozeného výrazu platí pro geometrickou představu o průběhu exponenciální funkce s ryze imaginárním exponentem? K tomu si vyjádřeme danou situaci pomocí následujícího obrázku:

Obr. 5. Geometrický význam exponenciální funkce s ryze imaginárním exponentem

Protože podle tohoto obrázku je

(27)

tak pro reálnou složku komplexního čísla které je vyjádřené ve složkovém kartézském tvaru, tj. a které má jednotkový modul, platí a podobně pro imaginární složku b tohoto komplexního čísla je Z toho plyne, že hodnoty exponenciální funkce s ryze imaginárním exponentem jsou v závislosti na hodnotě veličiny j vyjádřeny body na jednotkové kružnici v komplexní rovině.

Pro některé konkrétní hodnoty úhlu je atd.

Z formule Komplexní čísla (6), resp. Komplexní čísla (26), tj. že resp. z její varianty pro zápornou hodnotu úhlu j, tj. (při jejím odvození využíváme vlastností sudé funkce kosinus a liché funkce sinus) lze odvodit tzv. Eulerovy vztahy.