Fibonacciho posloupnost - nerekurzivní řešení

Při řešení nerekurzivním způsobem využijeme toho, že si můžeme pamatovat předchozí výsledky. Protože se k výpočtu dalšího prvku používají předchozí 2 prvky, tak si budeme pamatovat právě tyto 2 předchozí prvky. Nejprve ovšem musíme, stejně jako v rekurzivním způsobu řešení, ošetřit výsledné hodnoty pro a . Program tedy začne 2 podmínkami, ve kterých se bude s těmito hodnotami počítat a může se rovnou přejít k vypsání výsledku.

Nyní můžeme přistoupit k výpočtu dalších členů posloupnosti. Máme zadaný počet , do kterého máme posloupnost počítat, takže použijeme cyklus s daným počtem opakování. Pro první 2 hodnoty (0 a 1) jsme udělali na začátku programu podmínky, takže výpočet bude pro hodnoty 2 a vyšší, tj. rozmezí cyklu bude od 2 do .

Další prvek posloupnosti je součtem předchozích dvou. Hodnota , hodnota , hodnota atd. Z tohoto krátkého zápisu je vidět, že hodnota je dána součtem řekněme A a B. Pro další prvek posloupnosti se hodnotou B stává předchozí hodnota A a hodnotu A se stává předchozí vypočtená hodnota - hodnoty se "posouvají". Stejně tak i my je budeme posouvat.

Na začátku budeme mít nějaké a , což jsou předchozí 2 hodnoty. Pro další výpočet se musí provést posunutí těchto hodnot, a to tak, že do se přesune hodnota z a do se je přesune naposledy vypočtená hodnota prvku. Zbývá nám pouze určit počáteční hodnoty a . Ty jsou dány předpisem Fibbonaciho posloupnosti a jsou 1 a 0.

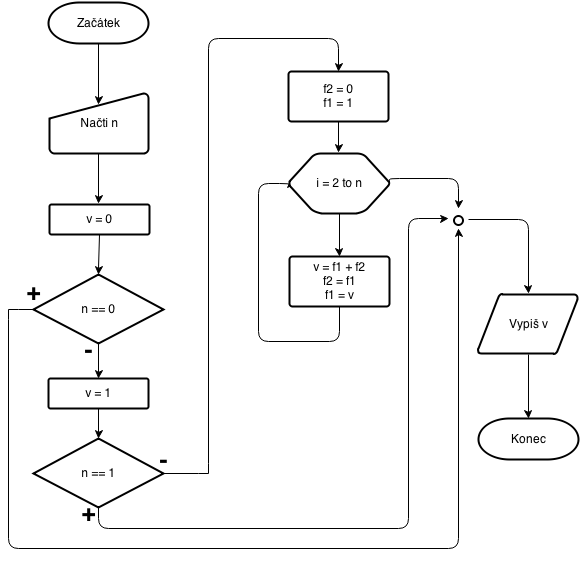Výsledek není tak přehledný jako v případě rekurzivního způsobu, ale eliminovali jsme všechny negativní vlastnosti, které rekurzivní způsob řešení sebou nesl. Každý prvek posloupnosti se počítá pouze jednou a nedochází k opakovanému vnořenému volání. Máme pouze 3 pomocné proměnné navíc.