
Složitost algoritmu
Složitost závisí na velikosti vstupních dat, tj. můžeme popsat jako funkci T(n), kde číslo n udává velikost vstupních dat. Např. T(n) = an + b, kde a, b jsou nějaké konstanty, je zápis lineární časové složitosti (složitost roste lineárně s rostoucí velikostí vstupů).
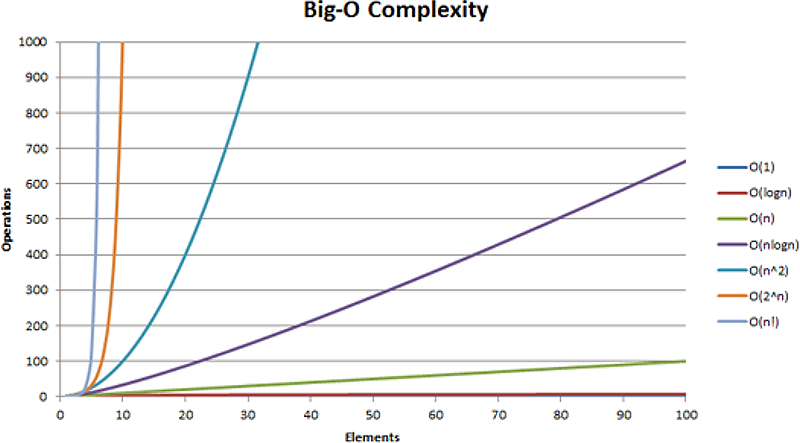
Obvykle je pro odhad složitosti důležitý pouze typ funkční závislosti a nikoliv přesné hodnoty konstant, ty se zanedbávají. Efektivními algoritmy nazveme takové postupy, jejichž složitost je maximálně polynomiální (např. n127, nikoliv exponenciální např. 2n). Provádění exponenciálních algoritmů T(n) = 2n či dokonce algoritmů o složitosti T(n) = n! může už jen při malém navýšení velikosti vstupních dat trvat i mnoho tisíců a miliónů let. Ani polynomiální algoritmy s velkým stupněm polynomu nebo s velkými vstupními daty nejsou příliš rychlé, viz následující tabulka:
| n | log2(n) | n*log2(n) | n2 | n3 | 2n | n! | nn |
|---|---|---|---|---|---|---|---|
| 5 | 3 | 15 | 25 | 125 | 32 | 120 | 3 125 |
| 10 | 4 | 40 | 100 | 1 000 | 1 024 | 3 628 800 | 10.0E+9 |
| 20 | 5 | 100 | 400 | 8 000 | 1 048 576 | 2.43E+18 | 1.05E+26 |
| 50 | 6 | 300 | 2 500 | 125 000 | 1.13E+15 | 3.04E+64 | 8.88E+84 |
| 100 | 7 | 700 | 10 000 | 1 000 000 | 1.27E+30 | 9.33E+157 | 1.00E+200 |
| 200 | 8 | 1 600 | 40 000 | 8 000 000 | 1.61E+60 | ||
| 500 | 9 | 4 500 | 250 000 | 125 000 000 | 3.27E+150 | ||
| 1 000 | 10 | 10 000 | 1 000 000 | 1 000 000 000 | 1.07E+301 |
V zápisu T(n) = an + b je a multiplikativní konstanta, která v sobě zahrnuje počet operací, který je třeba provést na jednotku vstupních dat. Aditivní konstanta b udává pouze konstantní nárůst složitosti nezávislý na velikosti vstupních dat. Při značné velikosti vstupních dat můžeme konstanty a a b zanedbat, protože vzhledem k velikosti n jsou nepatrné, a výsledná složitost T(n) tak závisí především na velikosti n, tj. velikosti vstupních dat algoritmu.
Vybereme-li ze všech konstant a největší konstantu, kterou označíme c, platí T(n) ≤ cn pro všechna dostatečně velká n. Tuto skutečnost značíme T = O(n), čímž vyjadřujeme asymptotické chování funkce T. Horní odhad složitosti algoritmu Tworst(n) udává složitost algoritmu v nejhorším případě. Složitost algoritmu f(n) je asymptoticky menší nebo rovna g(n), tj. f(n) = O(g(n)), právě když existuje taková kladná konstanta c tak, že pro každou velikost dat n od určité hodnoty n0 platí: 0 ≤ f(n) ≤ cg(n).
Např.: 2n2 + 3n + 4 = O(n2), neboť pro n0 = 1 a c = 10 platí 2n2 + 3n + 4 <= cn2.
Dolní odhad složitosti Tbest(n) určuje minimální složitost daného algoritmu (nejkratší čas provedení), která nastává jen pro určité případy vstupních dat. Pokud o algoritmu víme, že má dolní odhad složitosti n2, je jasné, že výsledek nedostaneme rychleji než v kvadratickém čase: Složitost algoritmu f(n) je asymptoticky větší nebo rovna g(n), tj. f(n) = Ω(g(n)), právě když existuje taková kladná konstanta c tak, že pro každou velikost dat n od určité hodnoty n0 platí: 0 ≤ cg(n) ≤ f(n).
Např. zápis Tbest(n) = Ω(n3) udává kubickou dolní složitost algoritmu.
Složitost v průměrném případě (očekávaná složitost) Tavrg(n) se počítá jako střední hodnota náhodné složitosti T(n) při nějakém rozložení vstupních dat. Někdy může být i řádově lepší než složitost v nejhorším případě.
Řekneme, že složitost algoritmu f(n) je asymptoticky stejná jako g(n), tj. f(n) = Θ(g(n)), právě když existují takové kladné konstanty c1,c2 tak, že pro každou velikost dat n od určité hodnoty n0 platí: 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n).
Algoritmus je pro danou úlohu optimální, jestliže neexistuje algoritmus, který by tuto úlohu řešil v nejhorším případě s menším počtem základních operací. Často se místo Tworst(n) odhaduje pouze podle toho, kolikrát se provedou některé základní, časově nejnáročnější operace. Většinou existuje tzv. triviální dolní odhad, což je velikost instance, protože algoritmus musí vždy projít celý vstup alespoň jednou.




