Úlohy k procvičení

ÚLOHA 1: Vypočtěte a nakreslete frekvenční charakteristiku jednoduchého systému, který počítá diference dvou posledních vzorků časové řady a má rovnici:

Řešení

Frekvenční charakteristiku je možno vypočítat např. DTFT impulsní charakteristiky a využít Eulerových vztahů mezi komplexními exponenciálami a goniometrickými funkcemi. Amplitudovou frekvenční charakteristiku ukazuje obrázek 2.4.

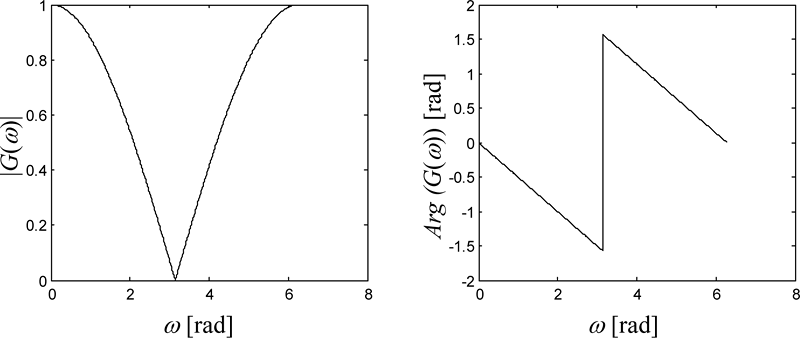
Obr. 2.4:  (Úloha 2) – Modulová (vlevo) a fázová (vpravo) frekvenční charakteristika systému, který počítá diference z posledních dvou vzorků časové řady na vstupu.

ÚLOHA 2: Vypočtěte a nakreslete frekvenční charakteristiku jednoduchého systému, který počítá průměr dvou posledních vzorků časové řady a má rovnici:

 

Řešení

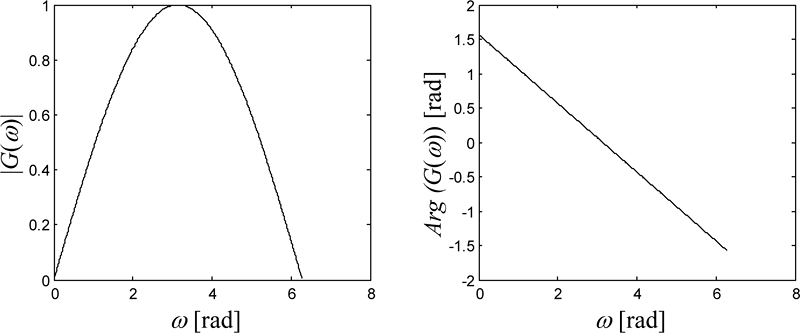
Frekvenční charakteristiku je možno vypočítat např. DTFT impulsní charakteristiky a využít Eulerových vztahů mezi komplexními exponenciálami a goniometrickými funkcemi. Amplitudovou frekvenční charakteristiku ukazuje obrázek 2.5.

 

Obr. 2.5: (Úloha 3) – Modulová (vlevo) a fázová (vpravo) frekvenční charakteristika systému, který počítá průměry z posledních dvou vzorků časové řady na vstupu.

ÚLOHA 3: Vyzkoušejte si demonstrační aplikaci pro operátor konvoluce „Joy of convolution“ na této URL: http://www.jhu.edu/~signals/discreteconv2/index.html

ÚLOHA 4: Realizujte v MATLABu vlastní funkci pro výpočet konvoluce pomocí cyklu, násobení a sčítání. Porovnejte výsledky z Vaší implementace s výsledky z matlabovské funkce conv(). Otestujte, zda je operátor konvoluce komutativní.

Řešení

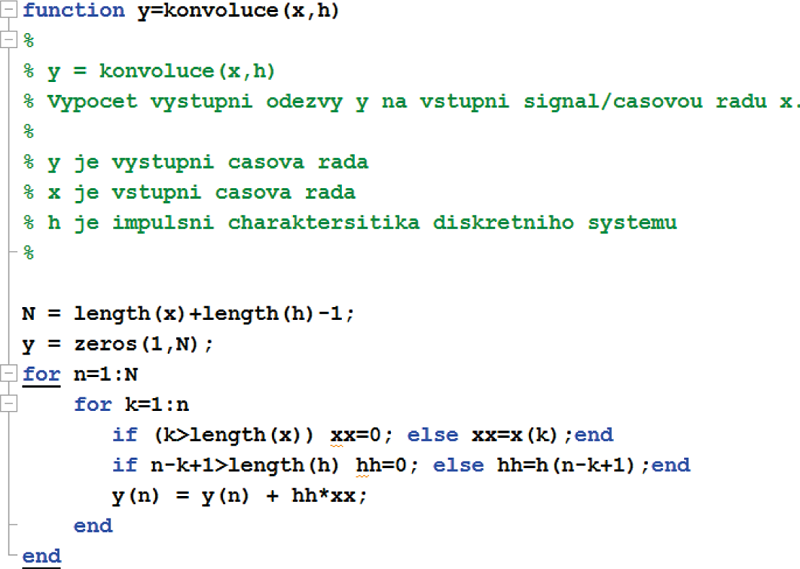
Jedna z možností, jak realizovat funkci konvoluce, je uvedena v kódu níže.

Komutativitu lze ověřit součtem absolutních hodnot rozdílů výstupů z konvoluce při různém pořadí vstupních argumentů – tento součet:

sum(abs(conv(x(:),h(:))-conv(h(:),x(:))))

by měl být nulový.