Exponenciální vyhlazování a predikce

Exponenciální vyhlazování je postup pro kontinuální revizi predikce s využitím nejnovějších hodnot modelované časové řady. Starším vzorkům se přiřazují exponenciálně klesající váhy, a tak se na výpočtu predikované hodnoty pozorované časové řady podílejí její novější vzorky větší vahou než ty starší. Kromě modelování či predikce se využívá exponenciální vyhlazování také za účelem potlačení náhodného rušení ve zpracovávané časové řadě.

Výpočet krátkodobé predikce časové řady pomocí exponenciálního vyhlazování je dán rekurentní rovnicí [2]:

(6.43)

ve které představuje  hodnotu vyhlazené časové řady a zároveň je i predikcí pro její příští vzorek x(n+1). Parametr a, který se označuje také jako koeficient zapomínání, má vliv na exponenciální pokles vah, pomocí kterých je vlastně realizován vážený průměr ze všech předchozích vzorků, neboť (6.43) lze přepsat také na [2]:

Za iniciální hodnotu  se dosazuje první hodnota časové řady x(0) nebo někdy také průměr několika prvních pozorovaných vzorků časové řady.

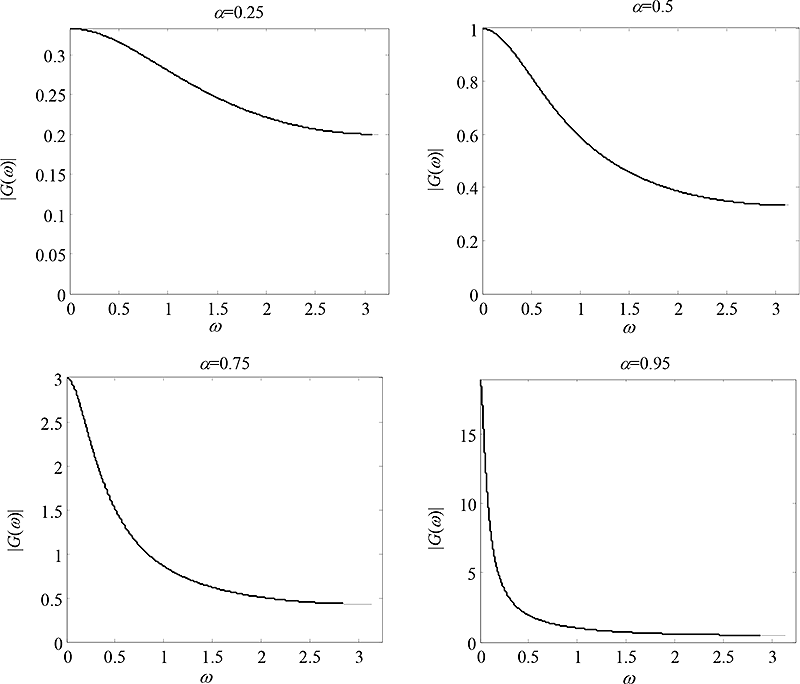
Obr. 6.3: Modulové frekvenční charakteristiky filtrů IIR pro realizaci exponenciálního vyhlazování s různými hodnotami koeficientu zapomínání a.

Volba hodnoty koeficientu zapomínání a může být ponechána na optimalizační proceduře, která najde hodnotu a minimalizující střední kvadratickou chybu predikce pro konkrétní pozorovanou časovou řadu. Alternativně může být rozvaha nad hodnotou parametru a provedena ve frekvenční doméně. Exponenciální vyhlazování lze realizovat pomocí diskrétní soustavy se strukturou odpovídající filtru IIR s přenosovou funkcí H(z)=a / (1-az^-1). Obr. 6.3 ukazuje modulové frekvenční charakteristiky exponenciálního vyhlazování pro různé hodnoty a. Jde o dolní propusti lišící se mezi sebou šířkou propustného pásma. Je-li pro konkrétní aplikaci důležité předpovídat pouze pozvolné změny v trendu časové řady, pak bude pro predikční model zvolen koeficient a co nejblíže číslu 1. Pokud naopak bude v jiné aplikaci důležité předpovídat i děje s rychlou dynamikou, bude zřejmě zvolena nižší hodnota koeficientu a. Má-li být rozvaha ve frekvenční doméně smysluplná, je nutno do ní zahrnout také frekvenční spektrum pozorované časové řady.

Exponenciální vyhlazování se označuje někdy také jako model EWMA (exponentially weighted moving average). Výše v textu však bylo ukázáno, že exponenciální vyhlazování ve své originální podobě podle rovnice (6.43) se realizuje IIR filtrem, a podobá se tak více autoregresním modelům než modelům s klouzavým průměrem. Pokud se rovnice (6.43) přepíše do tvaru pro předpovídání formou korekce chyby predikce:

je evidentní, že exponenciální vyhlazování svou strukturou odpovídá modelu ARIMA(1,1,0). Označovat exponenciální vyhlazování jako model EWMA je tedy nevhodné^[1].