Úlohy k procvičení

ÚLOHA 1: Určete diferenční rovnici systému s přenosovou funkcí:

Řešení

• Po dlouhém vydělení polynomu polynomem dojdeme k výrazu se zápornými mocninami z a inverzní Z transformací získáme požadovanou diferenční rovnici.

  

            

  

  

           

• Jiný způsob řešení, který nevyžaduje obtížné dělení polynomu polynomem:

  

  

  

  

ÚLOHA 2: Je dán filtr s přenosovou funkcí .

Otázky:

1. Jedná se o filtr MA, AR nebo ARMA?
2. Je tento filtr stabilní?

Řešení

Po krácení polynomů je získána přenosová funkce ve tvaru jediného polynomu:

Jedná se tedy o filtr MA, který je stabilní, což lze ukázat na jeho přenosové funkci, která má po vykrácení dva nulové body (n₁=-j, n₂=+j) a čtyřnásobný pól v počátku (p_1..4=0). Pokud by byl filtr ovšem realizován podle původní nekrácené přenosové funkce, tj. s algoritmem ARMA, nešlo by zaručit stabilitu takového filtru, neboť vzhledem k pólům (p₅=1, p₆=-1) by se takto realizovaný filtr nacházel na mezi stability.

ÚLOHA 3: Je dán filtr s přenosovou funkcí .

Otázky:

1. Zjistěte diferenční rovnici systému.
2. Zjistěte impulsní charakteristiku systému.
3. Nakreslete rozložení nulových bodů a pólů.
4. Odhadněte amplitudovou frekvenční charakteristiku.
5. Na závěr vše ověřte v MATLABu pomocí funkce freqz().
6. O jaký filtr jde (HP, DP, PP) ?

Řešení

Pro přenos na nulové úhlové frekvenci platí, že . Chceme-li mít modul přenosu na nulové frekvenci jednotkový, pak . Po dosazení do rovnice pro přenosovou funkci systému a aplikováním inverzí transformace Z dostaneme diferenční rovnici filtru.

Z diferenční rovnice vyplývá, že jde o systém bez zpětných vazeb, tedy MA, a pro něj lze psát přímo impulsní charakteristiku:

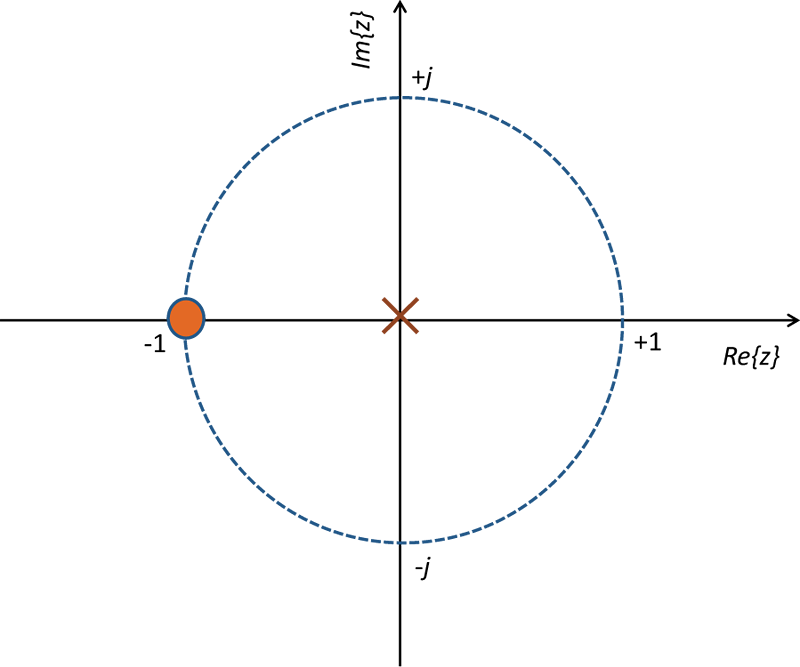
Z přenosové funkce ve tvaru součinu kořenových činitelů vyplývá, že vykreslujeme jeden nulový bod a jeden pól , viz obrázek 3.6.

Obr. 3.6:  (Úloha 2) – Rozložení nulových bodů a pólů přenosové funkce systému zadané v úloze 2.

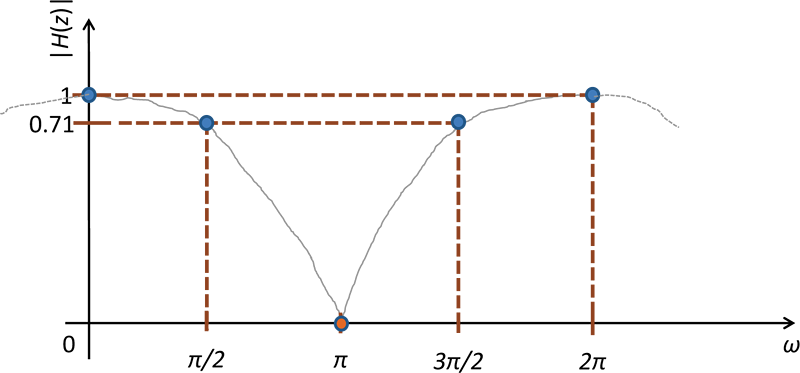
Při odhadu amplitudové frekvenční charakteristiky si vyznačíme na ose s úhlovou frekvencí její významné body na intervalu od 0 do 2π a v těchto bodech přenesených na jednotkovou kružnici vyhodnotíme vzdálenosti od nulových bodů a pólů. Z těchto vzdálenosti pak podle rovnice (3.5) vyhodnotíme přibližnou absolutní hodnotu přenosové funkce a vykreslíme do grafu. Vynesené body spojíme a výsledkem je jedna perioda amplitudové frekvenční charakteristiky, u níž je dobré si pamatovat, že se jedná o funkci spojitou a periodickou. Z tvaru této charakteristiky lze usuzovat, že jde o amplitudovou frekvenční charakteristiku filtru typu dolní propust, viz obrázek 3.7.

Obr. 3.7:  (Úloha 2) – Odhad tvaru modulové frekvenční charakteristiky systému zadaného v úloze 2.

Při ověřování správnosti našeho odhadu pomocí matlabovské funkce freqz() je nutno dát si pozor na to, jak se této funkci zadávají koeficienty přenosové funkce systému, což lze vyčíst z nápovědy. Zadáváme příkaz:

[H,W]=freqz([0.5, 0.5],[1],’whole’);

Následně vykreslujeme absolutní hodnoty komplexní přenosové funkce nad osou kódovanou ve vektoru W příkazem:

plot(W,abs(H));