Lineární časově invariantní systémy a periodické signály, frekvenční charakteristika,DTFT a DFT

Zesilování, zeslabování a fázový posuv harmonických složek zpracovávaných časových řad lze pro systém vyjádřit pomocí frekvenční charakteristiky , která je dána jako:

Z rovnice (2.6) lze usuzovat, že frekvenční charakteristika diskrétního systému je spojitou periodickou funkcí úhlové frekvence . Tato funkce je dána Fourierovou řadou s koeficienty, které odpovídají vzorkům impulsní charakteristiky popisovaného systému.

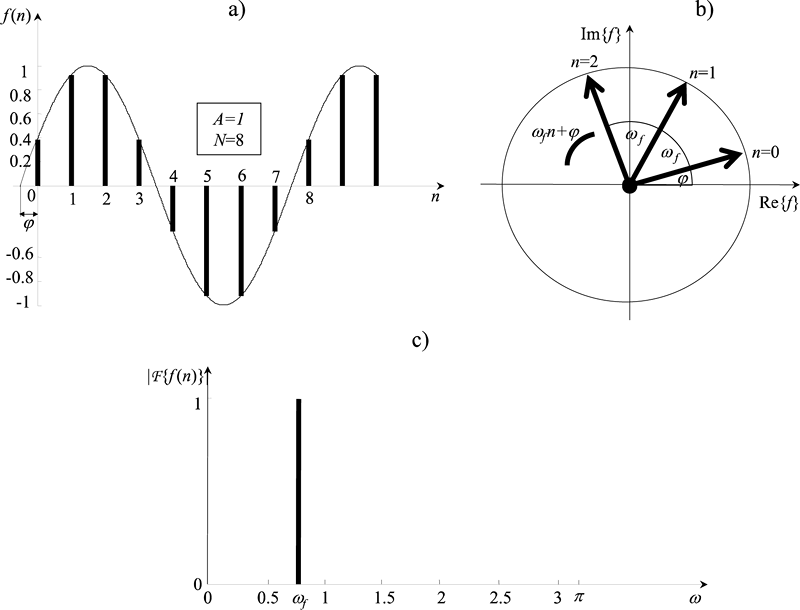
Obr. 2.2: Grafická znázornění harmonické časové řady a veličin, které určují její průběh. a) Harmonická časová řada. b) Rotující fázor v komplexní rovině. c) První půlperioda amplitudového frekvenčního spektra harmonické časové řady.

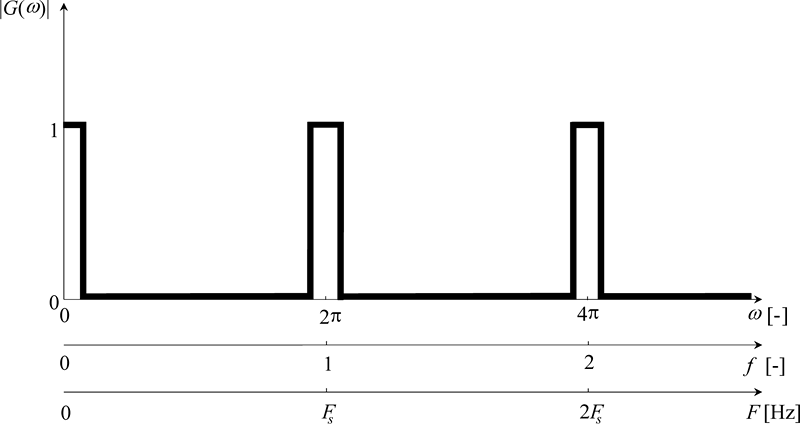
Perioda frekvenční charakteristiky s nezávislou bezrozměrnou proměnnou  je 2π, pro bezrozměrnou normalizovanou frekvenci  je perioda 1 a pro nezávislou proměnnou , kterou je frekvence v Hertzích, odpovídá perioda frekvenční charakteristiky hodnotě vzorkovací frekvence signálu , který je systémem zpracováván, viz příklad idealizované dolní propusti na obrázku 2.3.

Způsob, jakým systém preferenčně zesiluje či zeslabuje určité frekvenční komponenty zpracovávané časové řady a jakým způsobem tyto složky fázově zpožďuje, lze jistě považovat za důležitou součást popisu systému. Frekvenční charakteristika tedy vlastně tvoří popis systému ve frekvenční oblasti.

Pro doplnění je vhodné dodat, že Fourierova řada diskrétní posloupnosti je totéž co Fourierova transformace s diskrétním časem (DTFT – Discrete Time Fourier Transform) této posloupnosti, a je tedy možné říci, že frekvenční charakteristika systému odpovídá impulsní charakteristice tohoto systému transformované do frekvenční domény pomocí DTFT.

Obr. 2.3: Frekvenční charakteristika systému – modulová část. Jedná se zřejmě o systém, který představuje ideální dolní propust. Systém propouští harmonické komponenty v dolní části frekvenčního spektra (zesílení je 1) a utlumuje frekvenční komponenty v horní části frekvenčního spektra (zesílení je 0) – viz také obrázku 3.4. Frekvenční charakteristika je symetrická okolo normalizované úhlové frekvence π a periodická s periodou 2π. Obrázek zároveň ukazuje vztah mezi normalizovanou úhlovou frekvencí ω [-], normalizovanou frekvencí f=ω/2π=F/Fs [-]a mezi  frekvencí F [Hz].

Fourierova transformace s diskrétním časem DTFT by se však neměla zaměňovat nebo plést s diskrétní Fourierovou transformací (DFT – Discrete Fourier Transform). Zatímco DTFT produkuje z diskrétních posloupností spojité periodické funkce frekvence, viz (2.7) , výsledkem DFT je posloupnost konečného počtu vzorků DTFT, viz definice N-bodové DFT (2.8).

	(2.7)
	(2.8)

^[1] Pro objasnění rovnice (2.6) viz komentovaný  dotaz studenta.