
Řešená úloha
ÚLOHA 1: Sestavte model pro časovou řadu pozorovanou při měřeních koncentrace CO2 v ovzduší. Soubor dat, který je dostupný na: http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4411.htm obsahuje měsíční průměrné koncentrace CO2 na observatoři Mauna Loa v letech 1974 – 1987, viz tab 6.1. Koncentrace jsou udávány v bezrozměrných jednotkách, jako molární zlomek (mole fraction). Při konstrukci modelu využijte aditivní dekompozici společně s Boxovou-Jenkinsovou metodikou.
Načtení dat, jejich vykreslení, analýza trendu a periodických komponent byla pro tento datový soubor vyřešena ve výukové jednotce Náhodné procesy a a modely časových řad - dekompozice: Úloha 1. Pro následující konstrukci stacionárního modelu budou zvažovány obě varianty nesystematické složky časové řady x(n): 1. posloupnost xd(n), která se od původní časové řady liší pouze odečteným trendem a 2. posloupnost xd12(n), kterou od původní x(n) odlišuje navíc i sezónní diferencování o 12 vzorků.
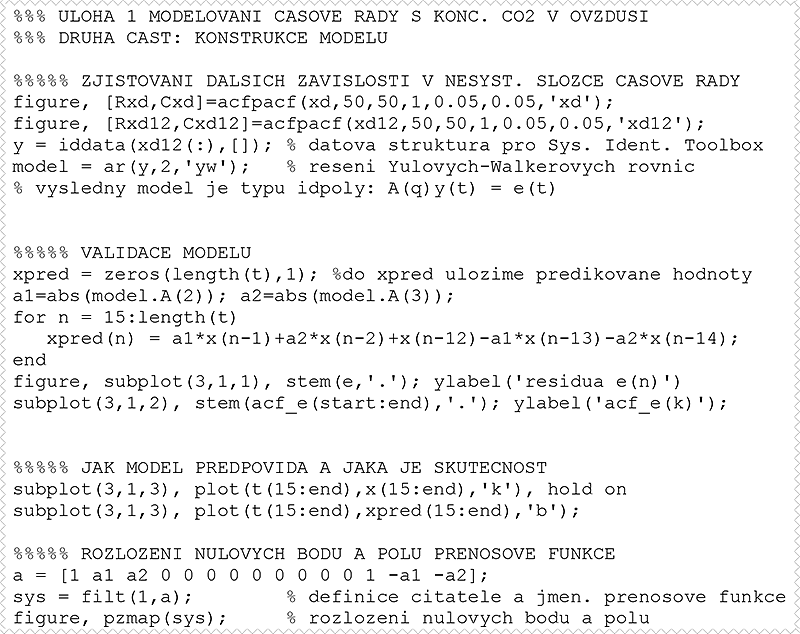
Obr. 7.7: Úloha 1 – modelování časové řady s měsíčními koncentracemi CO2.
Konstrukce modelu a jeho validace s využitím balíčku funkcí
System Identification Toolbox pro Matlab.
Ve skriptu, jehož programový kód je na obr. 7.7, se zjišťují závislosti v nesystematické složce časové řady x(n), a to pomocí autokorelační a parciální autokorelační funkce, viz obr. 7.8. Obě funkce zároveň slouží k určení řádů p, q členů AR(p) a MA(q) ve stacionárním modelu ARMA. Autokorelační funkce posloupnosti xd(n) potvrzuje výskyt periodické složky s periodou 12 vzorků – o posloupnosti xd(n) tedy nelze hovořit jako o náhodné, nesystematické časové řadě. Autokorelační funkce posloupnosti xd12(n) vykazuje tvar tlumené vlny, a tak lze tuto posloupnost modelovat pomocí autoregresní soustavy. Řád této soustavy lze vyčíst z bodu useknutí v parciální autokorelační funkci, který nastává pro zpoždění k0=2.
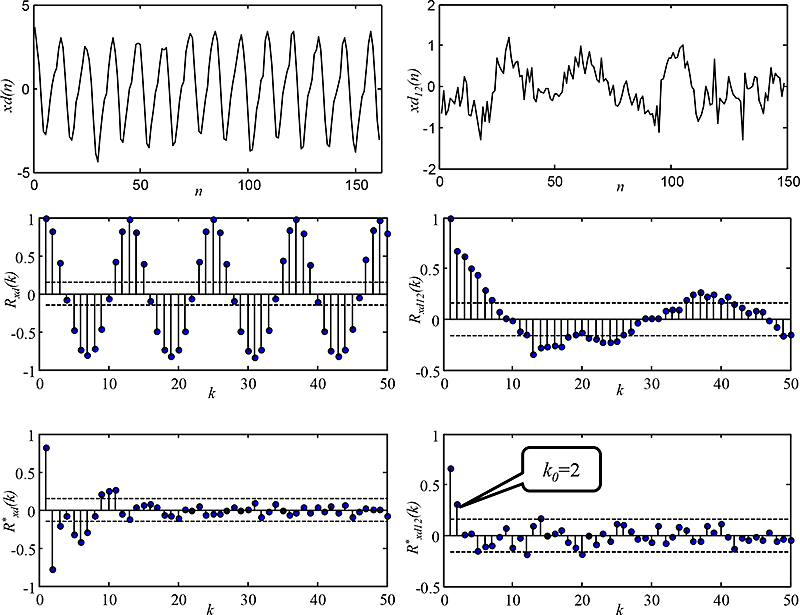
Obr. 7.8: Úloha 1 – Zjišťování závislosti mezi vzorky v nesystematické složce pomoci autokorelační funkce R(k) a parciální autokorelační funkce R*(k).
Odhad parametrů modelu AR(2), provedený pomocí Yulových-Walkerových rovnic, vede na konstrukci stacionárního modelu:
|
|
|
|
|
Stacionární model je třeba upravit na nestacionární, a to zpětným promítnutím všech úprav, které byly provedeny při stacionarizaci původní časové řady x(n), viz dále.
|
|
|
|
|
|
Rovnice výsledného AR(14) modelu má tvar:
|
|
|
|
|
|
Na obr. 7.9 jsou znázorněny tři kroky validace modelu formou grafické analýzy reziduí neboli chyb predikce. Autokorelační funkce chybové posloupnosti Rnn(k) se přibližuje autokorelační funkci bílého šumu. Část variability dat, kterou nebylo možné postihnout modelem, je tedy velmi náhodná.
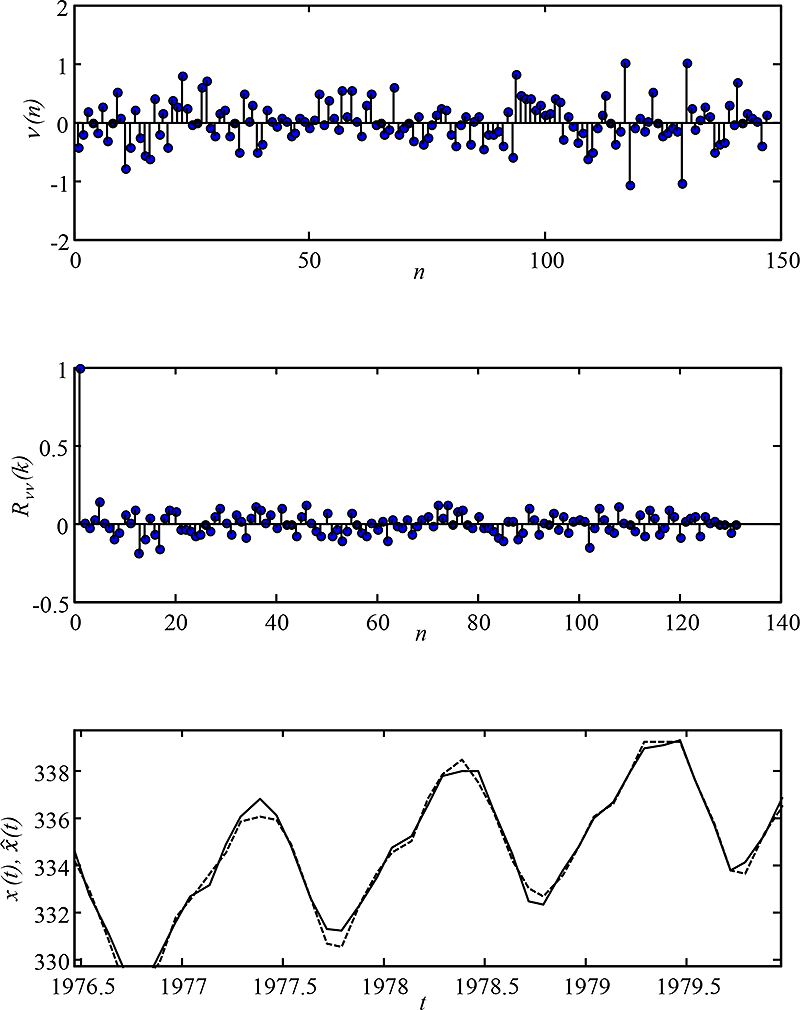
Obr. 7.9: Úloha 1 – Validace výsledného modelu zahrnuje a) grafickou analýzu residuí (neboli chyb predikce), b) včetně jejich autokorelační funkce a c) posouzení kvality předpovídání – vybrán detail, plná čára: x(n), přerušovaná čára: .
Obr. 7.10 ukazuje rozložení nulových bodů a pólů výsledného modelu AR(14) – několik pólů je vně jednotkové kružnice, a jedná se tedy o nestabilní soustavu. Tomu také odpovídá neustálý nárůst hodnot v časové řadě , která je modelem generována.
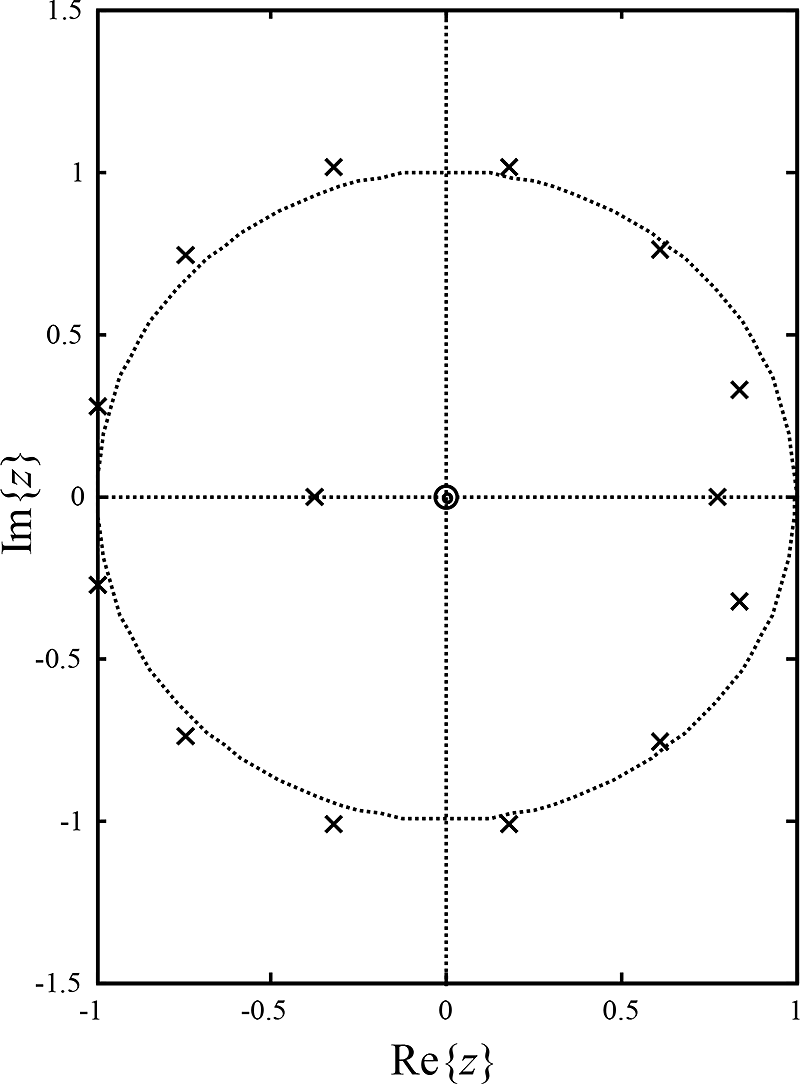
Obr. 7.10: Úloha 1 – Rozložení nulových bodů a pólů výsledného nestacionárního modelu AR(14).




