
Repetiční časové řady
Kumulační techniky se nejčastěji uplatňují u tzv. repetičních časových řad. Ty jsou charakteristické tím, že se v nich po nekonstantní době opakuje stejná, časově omezená posloupnost hodnot, která se označuje jako jedna repetice. Prakticky se lze setkat se dvěma různými typy repetičních časových řad:
- časové řady s repetiční povahou, které nelze považovat za perfektně periodické kvůli mezirepetiční variabilitě a nekonstantnímu zpoždění mezi jednotlivými repeticemi – např. diskrétní signály získané při měření aktivity srdce (signály EKG);
- časové řady získané opakovaným měřením stejného jevu – např. evokované potenciály v neurologii, viz obr. 5.2.
U repetičních časových řad prvního typu, které se někdy označují jako quasi-periodické, je nutno zajistit koherenci jednotlivých repetic neboli „lícování“ navzájem si odpovídajících vzorků jednotlivých repetic, viz obr 5.3. Stanovení referenčních souřadnic na časové ose lze provést např. jedním z těchto postupů (nebo pomocí jejich kombinace).
- Prahování. Za referenční časovou souřadnici se stanoví ta, na které hodnota posloupnosti v repetici poprvé přesáhne předdefinovaný práh.
- Detekce podle strmosti. Za referenční časovou souřadnici se stanoví ta, která je ve středu intervalu, přes který dochází v posloupnosti k požadované změně. Vyhledávají se obvykle souřadnice s maximální strmostí (náběžné nebo sestupné hrany impulsů či vln – rychlé změny) nebo s minimální strmostí (plató vln – velmi pomalé nebo žádné změny).
- Detekce podle vzoru. Za referenční časovou souřadnici se stanoví ta, od které je posloupnost svými hodnotami nejblíže hodnotám předdefinované vzorové posloupnosti.
Vzorem může být např. vybraná reprezentativní repetice nebo i uměle sestrojená posloupnost, která má svým průběhem odpovídat užitečné složce časové řady v jedné repetici. Pro výpočet podobnosti lze použít celou řadu metrik – v nejjednodušším případě půjde zřejmě o nalezení minima sumy čtverců rozdílů mezi vzorovou posloupností a odpovídajícími vzorky ze zpracovávané časové řady.
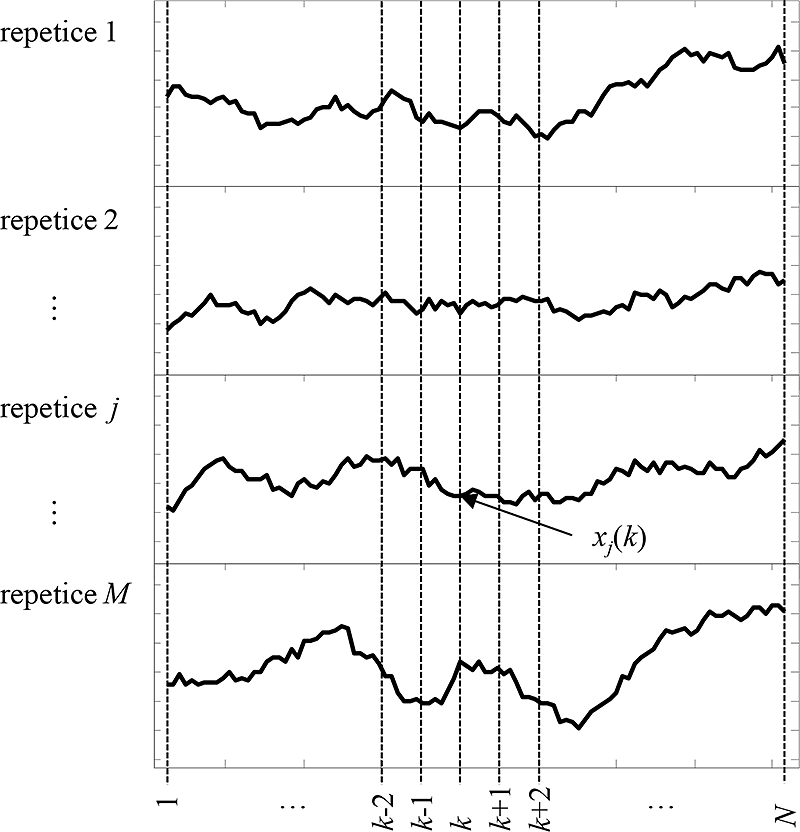
Obr. 5.3: Sada M repetic časové řady obsahující užitečnou a rušivou složku. Každá repetice je dána posloupností navzájem si odpovídajících vzorků xj(k), kde k=1,2,…,N.




