Dekompozice časových řad

Na problém modelování časových řad je možno pohlížet jako na analýzu směsí užitečných a rušivých komponent. Cílem modelování je oddělit užitečnou složku od náhodného rušení, přičemž užitečná (nebo také systematická) složka se v literatuře často ještě dělí na tzv. trendovou, sezónní a cyklickou složku. Je-li na směs užitečných a rušivých komponent pohlíženo jako na směs aditivní, pak lze časovou řadu x(n) zapsat ve tvaru:

(6.42)

kde v(n) je náhodná chyba nebo rušení, T(n) je trendová složka vyjadřující dlouhodobý nárůst nebo pokles hodnot časové řady, C(n) zastupuje sezónní i cyklickou složku, neboť obě tyto komponenty lze považovat společně za periodické kolísání hodnot časové řady.

Detailnější rozklad C(n) na složku sezónní a cyklickou lze najít zejména v literatuře věnující se chování ekonomických systémů a autoři rozlišují periodické složky na sezónní a cyklické podle délky periody: je-li perioda dlouhá den, týden, měsíc, kvartál nebo rok, bývá taková složka označovaná jako sezónní; nevykazuje-li perioda kalendářní charakter nebo je delší než jeden rok, pak se hovoří o složce cyklické. S ohledem na znalosti získané v kapitole Lineární časově invariantní systémy a periodické signály, Fourierova řada, o rozkladu periodických signálů nebo časových řad na harmonické komponenty pomocí Fourierovy řady, není třeba v tomto textu dále komplikovat názvosloví a složka C(n) zde bude označována jako periodická.

Kromě dekompozice aditivních směsí se někdy využívá také multiplikativní dekompozice. Zatímco v případě aditivního modelu jsou všechny složky vyjádřeny ve stejných jednotkách jako pozorovaná časová řada, v případě multiplikativního modelu je ve stejných jednotkách jako pozorovaná řada pouze trendová složka a ostatní (periodická složka a složka rušení) vyjadřují součinem relativní, okamžitý nárůst nebo pokles hodnot časové řady. Multiplikativní dekompozice je nad rámec tohoto učebního textu – dekompozice časových řad je zde probrána jen pro aditivní směsi.

Trendová složka je obvykle po grafické rozvaze vypočítána regresní analýzou, kdy je aplikací metody nejmenších čtverců proložen obecný polynom předem daného stupně nebo i jiná předem daná funkce (např. exponenciála, sigmoida aj.).

Detekce periodické složky může být provedena rozkladem na harmonické složky Fourierovou řadou (viz kapitola Lineární časově invariantní systémy a periodické signály, Fourierova řada) nebo pomocí autokorelačních a křížových korelačních funkcí.

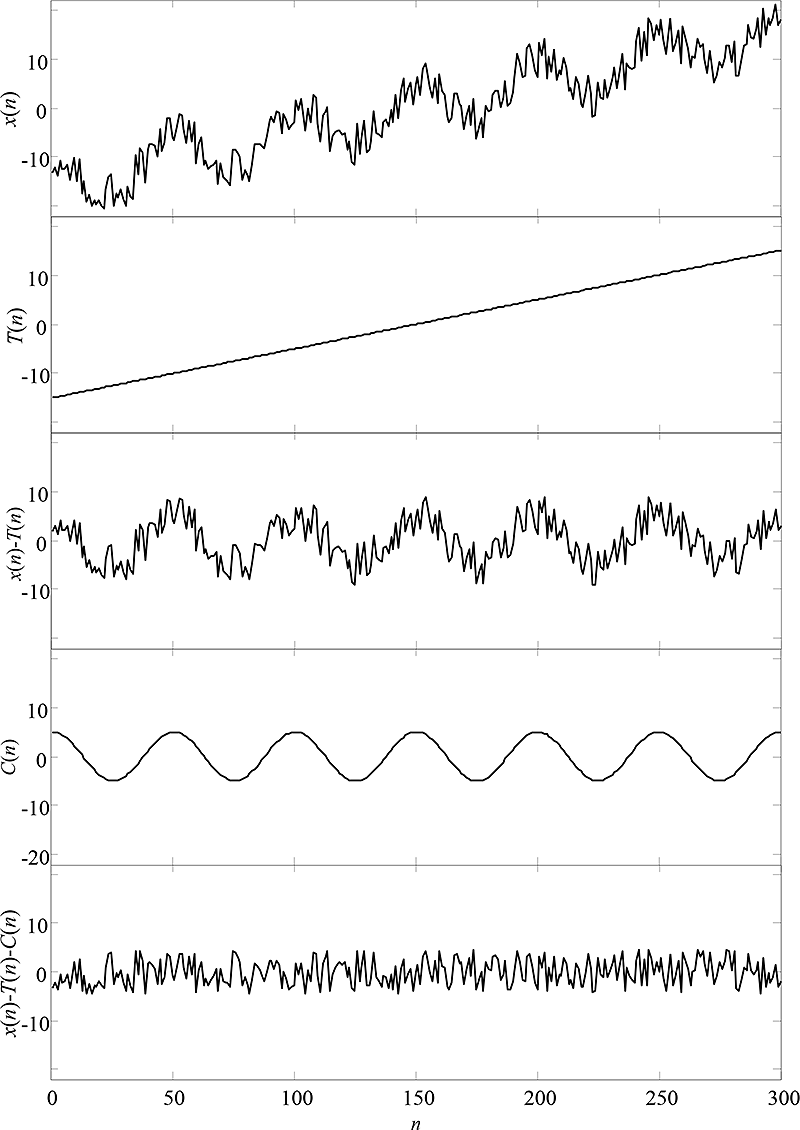
Obr. 6.2: Dekompozice časové řady x(n) na trendovou složku T(n), periodickou složku C(n)
a náhodné rušení v(n).

Obr. 6.2 ukazuje aditivní dekompozici časové řady x(n) na trendovou, periodickou složku a složku rušení. V ilustračním jednoduchém příkladu byla použita časová řada obsahující lineární trend a periodická složka obsahovala jedinou harmonickou. V praxi může být aditivní dekompozice časové řady ztížena komplexnější trendovou funkcí (např. lineární trend s několika body zlomu, lokální polynomické trendy apod.) a/nebo více nezanedbatelnými harmonickými komponentami v periodické složce.

Pokud složka rušení v(n), získaná očištěním časové řady od trendu a periodické složky, odpovídá realizaci bílého šumu, pak výsledek dekompozice dostatečně vysvětluje veškeré dynamické jevy zachycené v analyzované časové řadě. Pokud tomu tak není, což je v praxi velmi častý případ, znamená to, že složka rušení obsahuje ještě nezanedbatelné závislosti mezi vzorky a ty mohou být vysvětleny s využitím Boxových-Jenkinsových modelů stacionárních náhodných procesů, viz Náhodné procesy a modely časových řad - Boxovy a Jenkinsovy modely.