Kumulační zvýrazňování s exponenciálními vahami
Oba diskutované algoritmy kumulačního zvýrazňování s rovnoměrnými vahami pracují tak, že se ve výsledné kumulované repetici uplatňuje každá zpracovávaná repetice se stejnou vahou po dobu trvání M repetic, po té je zcela zapomenuta a více se s ní již nepracuje. Při kumulačním zvýrazňování s exponenciálními vahami se ve výsledku uplatňuje každá zpracovaná repetice, a to s klesající váhou do minulosti [3]:
|
|
(5.16) |
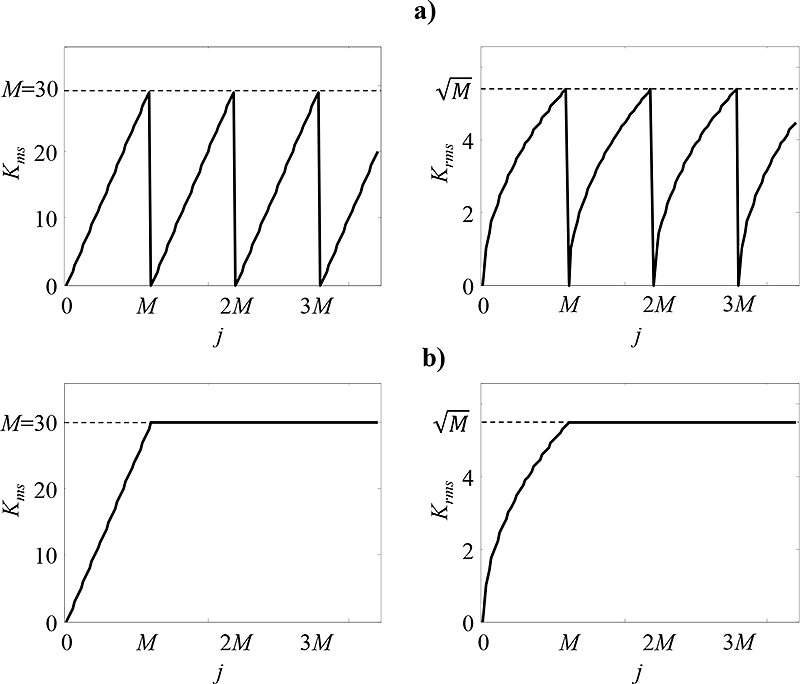
Obr. 5.6: Dynamické vlastnosti kumulačního zvýrazňování s rovnoměrnými vahami pro M=30:
a) s pevným oknem, b) s klouzavým oknem.
Po dosazení exponenciálních vah do vztahu pro výpočet zlepšení poměru signálu k šumu (5.10) a (5.11) lze při znalosti vzorce pro výpočet součtu geometrické řady dospět k:
|
|
(5.17) |
|
|
(5.18) |
kde zjednodušené vztahy pro výkonové zlepšení poměru signálu k šumu Kms a pro amplitudové zlepšení poměru signálu k šumu Krms lze aplikovat při vysokých počtech zpracovaných repetic M. Lze tedy usoudit, že pro velké počty repetic M bude výsledek exponenciálního kumulačního zvýrazňování závislý pouze na koeficientu a.Za účelem dosažení co největšího průměrného zlepšení poměru signálu k šumu bude snahou nastavit koeficient a na číslo blížící se k 1, avšak je nutné si uvědomit, že v takových případech se na výsledné kumulaci nezanedbatelně podílí mnohem více repetic, a tedy i mnohem více starších repetic, než v případě, kdy je a nižší, a kdy tedy vliv starších repetic vlivem geometrické řady v (5.16) rychle klesá. Volba koeficientu a bude proto vždy kompromisem mezi dosažitelným zlepšením poměru signálu k šumu a schopností exponenciálního kumulačního zvýrazňování reagovat na eventuální změny[1] probíhající v užitečné složce zpracovávaných časových řad. Volbu hodnoty koeficientu a lze např. podmínit požadavkem na stejné průměrné zlepšení poměru signálu k šumu, jako je dosažitelné v případě kumulační metody s rovnoměrnými vahami a předvoleným počtem repetic M:
|
|
(5.19) |
Jiným východiskem pro volbu hodnoty koeficientu a může být i posouzení jeho vlivu na vlastnosti kumulačního zpracování ve frekvenční doméně. Pro konečný počet M repetic odpovídá posloupnost vah aj podle (5.16) hodnotám impulsní charakteristiky FIR filtru řádu M, kterým je v rámci kumulačního zpracování vlastně filtrováno N posloupností k-tých vzorků xj(k) z jednotlivých repetic. Obr. 5.7 ukazuje vliv hodnoty a na tvar modulové frekvenční charakteristiky takového filtru. Z obrázku je patrné, že uvedený filtr vykazuje vlastnosti dolní propusti, u které hodnota a ovlivňuje šířku propustného pásma. Při zvyšujícím se počtu repetic M se prodlužuje impulsní charakteristika filtru. Pokud roste počet repetic do nekonečna, je možné filtraci N posloupností k-tých vzorků xj(k) z jednotlivých repetic zajistit rekurzivním algoritmem, kterému odpovídá filtr IIR s přenosovou funkcí H(z)=a/(1-az-1). Frekvenční charakteristiky takového filtru jsou zobrazeny pro různé hodnoty koeficientu a v jedné z dalších výukových jednotek na obr. 6.3. Pro vyšší hodnoty a filtr lépe potlačuje složky, které představují mezirepetiční variabilitu a má tendenci propustit pouze ty složky, které se mezi repeticemi nemění vůbec nebo jen velmi pozvolna.
Na obr. 5.8 jsou znázorněny dynamické vlastnosti kumulačního zvýrazňování s exponenciálními vahami – přímé srovnání s dynamickými vlastnostmi kumulačního zvýrazňování s rovnoměrnými vahami je předmětem řešené úlohy 1. Porovnáním obr. 5.6 a obr. 5.8 lze dojít k závěru, že se exponenciální kumulace svými vlastnostmi více podobá rovnoměrné kumulaci s klouzavým oknem a má přitom velmi jednoduchý algoritmus, který nevyžaduje složité operace posunu v paměťovém poli repetic, jako je tomu u algoritmu rovnoměrné kumulace s klouzavým oknem a přitom umožňuje, stejně jako rovnoměrná kumulace s klouzavým oknem, sledování pomalých změn v užitečné složce zpracovávaných časových řad.
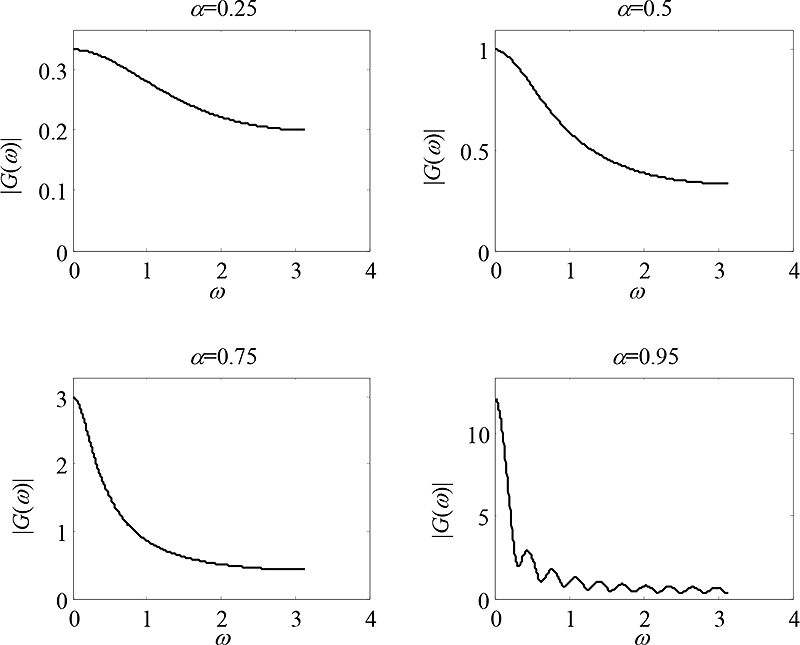
Obr. 5.7: Modulové frekvenční charakteristiky FIR filtru řádu M=20
s impulsní charakteristikou hj=aM-j+1pro různé hodnoty a.
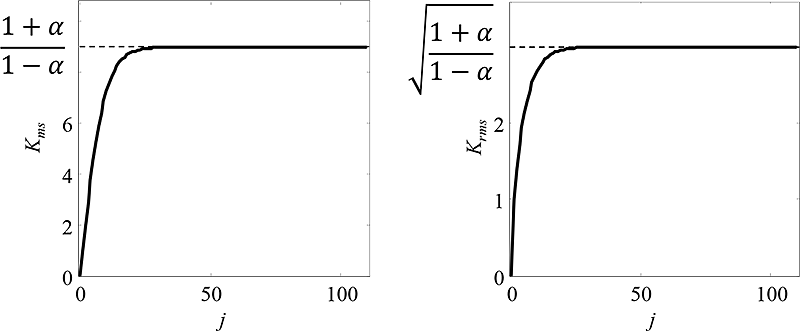
Obr. 5.8: Dynamické vlastnosti kumulačního zvýrazňování s exponenciálními vahami pro a=0,8.
[1] Při kumulačním zvýrazňování užitečné složky repetičních časových řad se obvykle předpokládá, že se užitečná složka mezi repeticemi nemění, nicméně v reálných aplikacích lze pomalé změny v užitečné složce očekávat, a na tyto trendy by mělo proto reagovat i kumulační zpracování.