Lineární časově invariantní systémy, konvoluce

Lineární časově invariantní (LTI – linear time invariant) systémy disponují matematickými vztahy mezi jejich vstupními a výstupními signály či časovými řadami. Pomocí nich lze určit výstupní odezvu LTI systému na jakýkoli vstup a lze také určit vstup systému při pozorování jeho výstupu. Operaci, která určuje vztah mezi časovými řadami na vstupu a výstupu LTI systému, se říká konvoluce. Pro její odvození pomocí základních matematických operací je třeba přijmout následující poučku, kterou lze selským rozumem vyvodit z vlastností LTI systémů.

POUČKA ODVOZENÁ SELSKÝM ROZUMEM:
„Známe-li odezvu LTI systému na velmi krátkou časovou řadu, můžeme pomocí těchto velmi krátkých řad seskládat libovolně dlouhou časovou řadu, a odezvu LTI systému na ni pak seskládat pomocí známé odezvy na velmi krátkou řadu.“

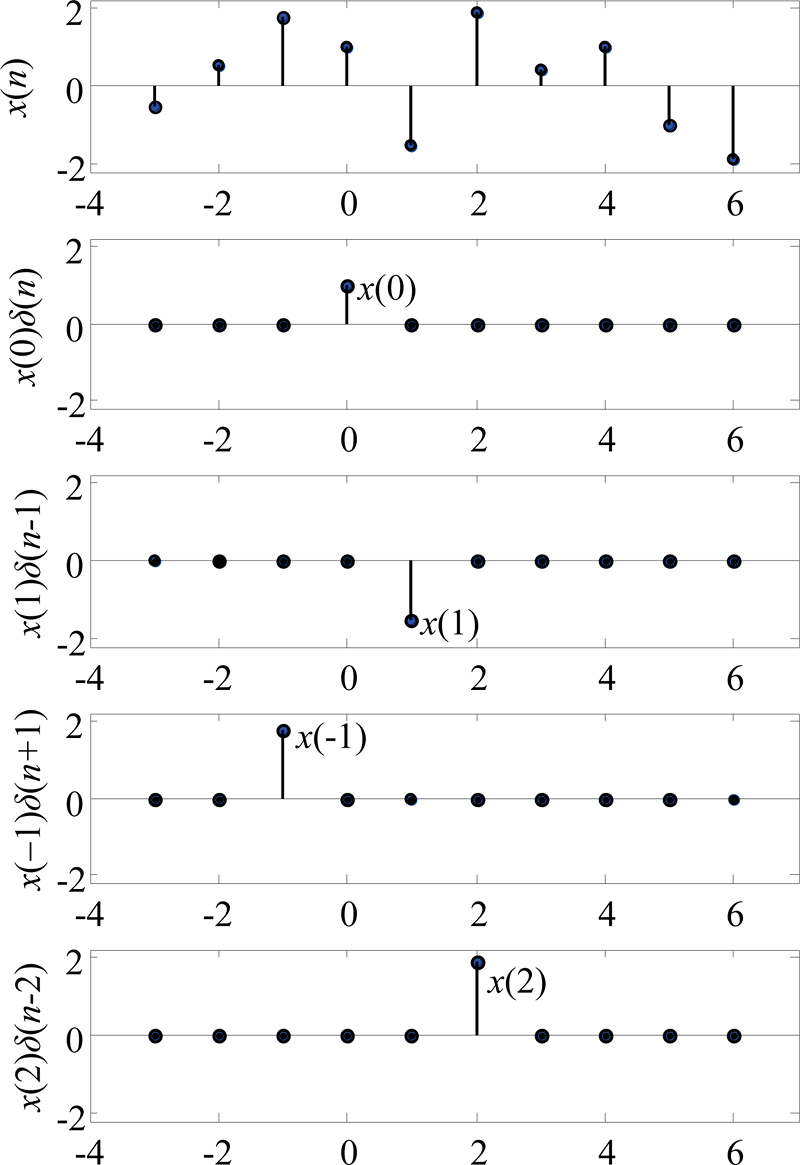
Nejkratší časovou řadou, kterou je možno pro tento účel použít, je jednotkový impuls , kterému ve spojité časové doméně odpovídá Diracova distribuce. Kombinací posunutých jednotkových impulsů lze sestrojit libovolnou časovou řadu, viz obrázek 2.1, což je možno také vyjádřit následující rovnicí:

Obr. 2.1: Sestrojení časové řady  pomocí jednotkových impulsů .

Za předpokladu, že odezvou LTI systému na jednotkový impuls je posloupnost , lze při aplikaci výše uvedené poučky, odvozené selským rozumem, vyjádřit odezvu LTI systému na časovou řadu takto:

Protože pro časově invariantní systém můžeme jistě říci, že jeho odezvy na časově posunuté jednotkové impulsy budou mít všechny stejný průběh a budou se lišit pouze právě časovým posunem. Můžeme tedy psát, že:

	(2.3)

Poslední výraz v rovnici (2.3) se označuje jako konvoluční suma a operátor konvoluce představuje matematický způsob výpočtu odezvy LTI systému na libovolnou časovou řadu při znalosti odezvy  tohoto systému na jednotkový impuls . Tato odezva se nazývá impulsní charakteristika systému a představuje jeden ze základních způsobů neparametrického popisu systému v časové nebo prostorové doméně.